Opgave 5

I topologioptimering ser man på funktioner af mange variable, men i denne opgave nøjes vi med at se på en funktion i to variable:

Afsat i et 3-dimensionalt koordinatsystem vil punkterne af formen udgøre en flade. Vi begrænser os til x - og y -værdier mellem 0 og 20 og kan sammenligne fladen med et bjerglandskab. På figuren er vist nogle niveaukurver for fladen.

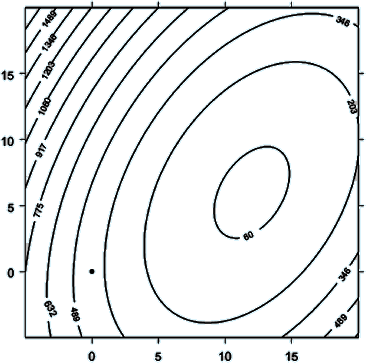
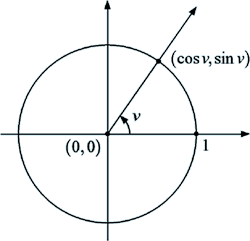
Vi forestiller os, at vi står på ski i dette landskab og befinder os i (0,0). Vi vil gerne nedad til det laveste punkt så hurtigt som muligt, men kan kun se en meter i hver retning. Man kan undersøge, i hvilken retning det går mest nedad ved at se på, hvordan højden varierer over punkter, der ligger på en cirkel med centrum i (0,0) og radius 1. Punktets position afhænger af vinklen v, som vist på figuren:

Man kan altså undersøge funktionen .

a) Tegn grafen for g på lommeregneren og find den vinkel, der giver den laveste højde. Sammenlign med niveaukurverne.

b) Overvej, hvordan man på tilsvarende måde trinvist kan komme til bunden. Hvordan bliver ruten i store træk?

Hvis man har differentialregning til rådighed kan minimumspunktet bestemmes direkte ved at finde ud af, hvor tangentplanen er vandret. Hertil skal man bruge de partielle afledede i et vilkårligt fast punkt: den partielle afledede med hensyn til x fås ved at differentiere med x som variabel og y som konstant. Hvis tangentplanen i kaldes α, og planen med ligningen kaldes β vil være lig med hældningen af skæringen mellem α og β. Tilsvarende med .

c) Bestem koordinaterne til minimumspunktet for f ved at løse ligningssystemet

Litteratur og URL'er: