- Find
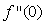 (og dermed krumningen i 0 for en parabel) når
- Opstil forskriften for den funktion, hvis graf er den nedre halvdel af en cirkel med centrum ( 0 , r ) og radius r, og beregn.
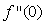- Vis at cirklen med radius 0,5 og centrum ( 0 , 0,5 ) er den størst mulige cirkel med centrum på y-aksens positive del, der har netop ét punkt fælles med parablen med ligningen y = x 2.
- C.V. Boys, Sæbebobler og de kræfter, der danner dem. Gyldendals kvantebøger (1962).
- F. Morgan, Proof of the Double Bubble Conjecture, Amer. Math. Monthly, March (2001) 193–205.
- NASA Microgravity Experiments: spaceflight.nasa.gov/station/crew/exp6/spacechronicles.html
- Normalsnittets krumning: 217.60.167.201/gc/nsnit.pdf
Denne indeholder blandt andet bevis for, at middelkrumningen ikke afhænger af, hvordan de ortogonale snit lægges.
|
|
