Vi ser i det følgende kun på brøker med positive hele tal i tæller og nævner.
- Vis at
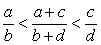 hvis hvis 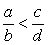
- To brøker
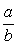 og og 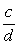 kaldes naboer, hvis kaldes naboer, hvis 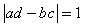 . .
Vis at 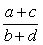 er nabo til både er nabo til både 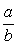 og og 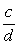 , hvis , hvis 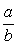 og og 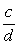 er naboer. er naboer.
- Vis at en brøk i intervallet mellem to naboer
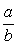 og og 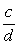 vil have en nævner, der er større eller lig med både b og d. vil have en nævner, der er større eller lig med både b og d.
- Gør rede for, at
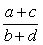 er den brøk med mindst mulig nævner, der ligger i intervallet mellem to naboer er den brøk med mindst mulig nævner, der ligger i intervallet mellem to naboer 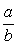 og og 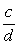 . .
- Vis for eksempel ved induktion, at to på hinanden følgende brøker i rækken
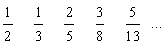 (1) (1)
er naboer.
- Betragt Fibonaccifølgen f(n), hvor f(1) = f(2) = 1 og f(n+1) = f(n) + f(n-1) for alle naturlige tal n større end 1. Altså følgen 1, 1, 2, 3, 5, 8, 13, …
Antag at brøkerne 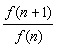 har grænseværdien har grænseværdien 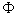 , når n går mod uendelig. , når n går mod uendelig.
Gør rede for, at 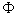 må være løsning til ligningen må være løsning til ligningen 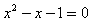 , og beregn den løsning, der er større end 1. , og beregn den løsning, der er større end 1.
- Vis at rækken (1) må gå mod
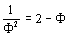 , når n går mod uendelig (med samme forudsætninger som i opgave f ) , når n går mod uendelig (med samme forudsætninger som i opgave f )
- Forklar hvorfor spiralerne med for eksempel antallet 21 drejer modsat dem med antallet 34.
|
|