En plads i solen - bruger naturen matematik?

Hvorfor danner solsikkens frø et mønster med 34 kurver med uret og 21 kurver mod uret?

Når man ser på en solsikkes blomsterstand, fanges øjet af nogle spiraler, der både drejer venstre og højre om.

Hvorfor vokser frøene langs disse spiraler? Hvorfor er antallet af spiraler i forskellige solsikker netop 13, 21, 34 eller 55? Hvor kommer disse tal fra?

Model af en rose, hvor bladene er arrangeret på samme måde som solsikkens kerner. Hvert nyt blad er drejet 137,5° i forhold til det foregående.

Hvad der følger her, er blot antydningen af en forklaring. Den levende natur er ikke en matematisk opgave med et entydigt facit. Vi skal blot skitsere en matematisk model af væksten i en solsikkes blomsterstand. Inden for denne model kan vi komme nærmere på nogle svar på ovenstående spørgsmål.

En primitiv vækstmodel

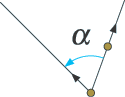En meget grov model af væksten i en solsikkes blomsterstand er følgende. Vi forestiller os, at frøene dannes ét ad gangen ud fra et centrum øverst i stilken og, når de første er dannet, flytter langsomt væk fra centrum langs en ret linje. Mellem retningerne for to på hinanden følgende frø er der en bestemt vinkel, som vi vil kalde drejningsvinklen.

Talværdien α af drejningsvinklen er, som vi skal se, helt bestemmende for det mønster, frøene danner. Lad os her måle drejningsvinklen som brøkdele af en hel cirkel, så svarer fx 90° til α = 1/4. Bemærk, at vi kun behøver at betragte mellem 0 og 1/2, da vi vil få samme mønster for α som for 1 - α. Hvis drejningsvinklen fx er 1/7, vil der fremkomme 7 stråler ud fra centrum.

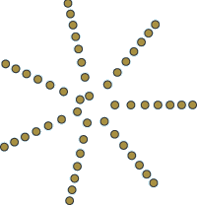Det ligner noget, der kunne blive til en rund blomsterstand. Der er dog det problem, at de 7 stråler kommer længere og længere fra hinanden, jo større blomsterstanden bliver, så der opstår områder, hvor der er langt mellem frøene. Og helt inde i centrum er der det problem, at når et frø er dannet, skal det næste frø dannes umiddelbart ved siden af.

Drejningsvinkel og spiraler

En måde at undgå dette sidste problem ville være at have en drejningsvinkel som et rationalt tal af formen p/q, hvor p og q er naturlige tal. Så får vi q stråler, men hver gang et frø er afsat, springer vi p stråler frem, før det næste afsættes. Ved at vælge p ca. halvt så stor som q, vil vi anbringe det næste frø så langt rundt om blomsterstanden som muligt.

Men se nu det mærkelige, der sker, hvis vi vælger drejningsvinklen til et tal som fx 11/23.

Der dannes 23 stråler, men nær centrum ser øjet slet ikke disse stråler, men derimod to spiraler! Det skyldes, at afstanden mellem frøene langs disse to spiraler er mindre end afstanden mellem frøene i de enkelte stråler. Og når frøene ligger tættere langs en kurve (her en spiral), end de gør langs stråler, fornemmer øjet kurven snarere end det større mønster. At vi nær centrum ser netop to spiraler skyldes, at drejningsvinklen 11/23 er tæt på at være 1/2.

Solsikken har udviklet en drejningsvinkel på

som kaldes den gyldne vinkel, og som med tre decimalers nøjagtighed er lig med 0,382, hvilket svarer til 137,5°. I en vis afstand fra centrum vil man kunne se 13 spiraler, fordi 5/13 er en god rational approximation med lille nævner til 0,382, hvilket betyder, at 13 på hinanden følgende frø i alt vil have beskrevet en drejning tæt på 5 omgange. Et nyt frø vil således blive afsat tæt på det frø, der blev afsat 13 frø tidligere.

Men hvorfor har solsikken udviklet en drejningsvinkel på 0,382? Vi har set, at rationale drejningsvinkler med lille nævner vil give dårlige pakninger af blomsterstanden. Før eller siden vil strålerne skilles ad, med dårlig udnyttelse af pladsen til følge.

Simple brøker

Vi kalder en brøk simplere end en anden, hvis nævneren er mindre. Ved valg af optimal drejningsvinkel skal man altså søge at undgå de simpleste brøker mest muligt. Man kan bruge dette princip til at konstruere en følge af brøker mellem 0 og 1/2, der nærmer sig den optimale drejningsvinkel.

Vi starter med den simpleste brøk 0/1, og vælger derefter den simpleste, der ligger længst muligt væk, nemlig 1/2. Den simpleste brøk mellem 0 og 1/2 er 1/3, og den simpleste brøk mellem 1/2 og 1/3 er 2/5. Således fortsættes og man får

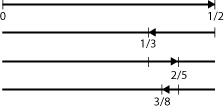
Hver ny brøk er den simpleste mellem de to foregående, og man kan vise, at den fås ved at addere henholdsvis tæller og nævner for de to foregående. Vi bemærker, at tællere og nævnere er følger af de såkaldte Fibonacci tal, hvor hvert tal er summen af de to foregående. Hvis rækken af brøker fortsættes, går brøkerne mod .

Pakningen ser nu således ud.

Den gyldne vinkel og evolution

Hvis vi ser frøpakning som en evolutionsmæssig faktor, må vi forestille os, at de planter, der (mere eller mindre tilfældigt) er bedre til at pakke deres frø, i gennemsnit vil få flere afkom; og på denne måde forsvinder de mutationer, der pakker med uhensigtsmæssige vinkler, og de mutationer, der pakker tæt på den gyldne vinkel, vil få mange efterkommere. Da denne proces er foregået over millioner af år, ser vi i dag kun de pakningsperfekte solsikker. At nye skud, frø, blade på stængler etc. vokser frem efter en drejning med den gyldne vinkel, og at der derved kommer Fibonacci tal frem som antal af spiraler, man tilnærmelsesvis kan se, er et fænomen, der også kan observeres i så vidt forskellige vækster som blomkål og grankogler.