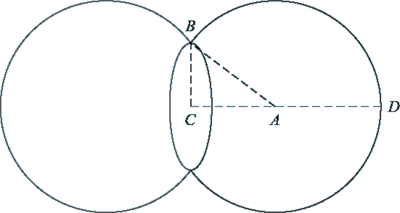
Vi vil se på en dobbeltboble med samme rumfang i de to kamre; væggen mellem kamrene er så en cirkelskive.
Med betegnelser som på figuren sættes r = | AB | og h = | CD |.
For en afskåret kugle med radius r og højde h gælder følgende formler for rumfanget V og den krumme overflade O:
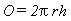 og
og 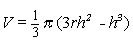
Vi vil nu holde rumfanget i de to kamre fast, men minimere den samlede overflade i dobbeltboblen ved at ændre på r og h.
Den samlede overflade, der består af de to krumme overflader og cirkelskivens areal, vil være en funktion af h, som betegnes f(h).
- Opstil en forskrift for f.
- Find ved differentiation et udtryk for sammenhængen mellem h og V, når f(h) er mindst mulig.
- Vis at h = 1,5 · r, når f(h) er mindst mulig.
- Vis at den stumpe vinkel mellem tangentplanerne i B til de to kugler er 120 grader, når den samlede overflade er mindst mulig.
- Vis den ovennævnte formel for rumfang af afskåret kugle ved at beregne rumfanget af et omdrejningslegeme ved integralregning (se eventuelt opgave 5.119 i Vejledende eksempler på eksamensopgaver i matematik, 3-årigt forløb til A-niveau).
Den ovennævnte formel for den krumme overflade af afskåret kugle kan udledes ved at benytte følgende formel for overfladen af et omdrejningslegeme: