Vi vil undersøge de to typer strømning og finde omslagspunktet mellem laminær og turbulent strømning mere præcist.
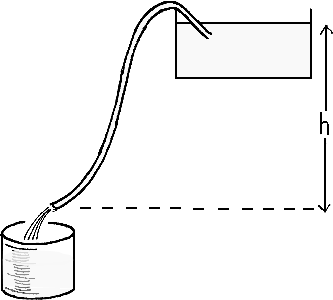 Eksperimentet kan gennemføres med en opstilling med vandkar, plastslange (som vist på figuren) og et måleglas. For varierende højdeforskelle mellem vandstanden i karret og slangens udløbsniveau – svarende til forskellige vandhastigheder – måles den tid, det tager at fylde måleglasset. Slangens dimensioner og måleglassets rumfang noteres også.
Eksperimentet kan gennemføres med en opstilling med vandkar, plastslange (som vist på figuren) og et måleglas. For varierende højdeforskelle mellem vandstanden i karret og slangens udløbsniveau – svarende til forskellige vandhastigheder – måles den tid, det tager at fylde måleglasset. Slangens dimensioner og måleglassets rumfang noteres også.
Fra formlen
rumfang = tværsnitsareal · længde kan længden af den vandslange, der skal til for at fylde måleglasset, beregnes. Endeligt kan vi med formen
længde = hastighed · tid beregne strømningshastigheden. Udregningerne kan med fordel foretages med lommeregnerens lister.
Til at illustrere hvordan strømningshastigheden ændrer sig med højdeforskellen, laves en (Δh, v)-graf.
Ved små højdeforskelle strømmer vandet laminært, ved store højdeforskelle strømmer det turbulent. Ud fra brøken  har fysikeren O. Reynolds fundet at omslagsområdet mellem de to strømninger kan beregnes til at være mellem 1 og 1,3. Her er r rørets radius, Δh er højdeforskellen og L er rørets længde (alle størrelser er angivet i mm).
har fysikeren O. Reynolds fundet at omslagsområdet mellem de to strømninger kan beregnes til at være mellem 1 og 1,3. Her er r rørets radius, Δh er højdeforskellen og L er rørets længde (alle størrelser er angivet i mm).
Brug Reynolds værdi til at beregne i hvilket højdeinterval, du vil forvente at finde omslaget for din slange. Stemmer det med dine målinger?
Ifølge teorien gælder at v og h er proportionale for laminært strømmende vand, og at v2 og h er proportionale for turbulent strømmende vand. Stemmer dette med din figur? Lav én regression, der passer til den første del af målepunkterne, og én anden regression, der passer til den anden del af målepunkterne.
Årsagen til at kurven knækker, når strømningen går over til at være turbulent, er, at modstanden i slangen øges. For os synes det måske uvæsentligt (vi sænker bare mundingen yderligere og sætter endnu mere fart på vandet), men for vandværkerne betyder det, at pumperne skal yde meget mere, hvis hastigheden bliver så stor, at vandet begynder at turbulere i rørene. Derfor tager man hensyn til det forventede vandforbrug, når man dimensionerer rørene fra vandværket til forbrugerne.
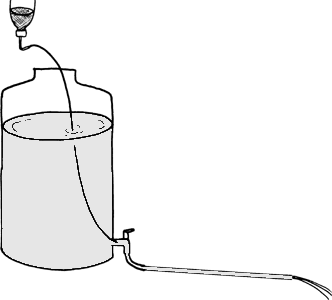
 Eksperimentet kan gennemføres med en opstilling med vandkar, plastslange (som vist på figuren) og et måleglas. For varierende højdeforskelle mellem vandstanden i karret og slangens udløbsniveau – svarende til forskellige vandhastigheder – måles den tid, det tager at fylde måleglasset. Slangens dimensioner og måleglassets rumfang noteres også.
Eksperimentet kan gennemføres med en opstilling med vandkar, plastslange (som vist på figuren) og et måleglas. For varierende højdeforskelle mellem vandstanden i karret og slangens udløbsniveau – svarende til forskellige vandhastigheder – måles den tid, det tager at fylde måleglasset. Slangens dimensioner og måleglassets rumfang noteres også. Hvor stort er vandtrykket i vandhanen?
Hvor stort er vandtrykket i vandhanen?