Dobbeltboblen - matematisk set

Hvis en kurve har en ligning af formen y = f(x) i et koordinatsystem, hvor x-aksen er parallel med kurvens tangent i punktet P, kan krumningen i P beregnes som f ’’(x_o) hvor x_o er førstekoordinaten til P.

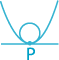
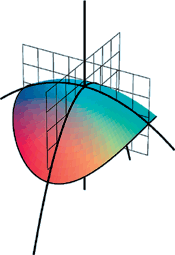Den dobbelt afledede i x_o udtrykker jo, hvor meget tangenthældningerne ændrer sig omkring x_o. Den numeriske værdi af krumningen er lig med 1/r, hvor r er radius af den cirkel, der følger kurven bedst muligt omkring P.

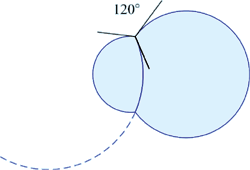Tværsnittet af en dobbeltboble består af tre cirkelbuer. Hvis radius for de tre cirkler kaldes henholdsvis r, s og R gælder:

Denne sammenhæng følger af, at middelkrumningen er lig med forskellen i tryk på hver side af sæbehinderne.

De tre tangenter i hvert af skæringspunkterne danner tre vinkler på hver 120°.