Opgave 1: Grundvandet på Tunø
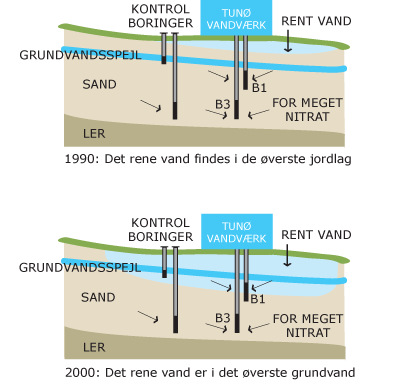
- Find den årlige nedsivning af vand på Tunø, angivet i mm/år.
Området omkring vandværket antages at være cirkulært. Den nævnte afstand er så radius i cirklen.
- Beregn den mængde vand, der hvert år siver ned til grundvandsmagasinet gennem området, angivet i m3/år.
- Siver der vand nok ned til at modsvare oppumpningen? Sammenlign med vandværkets oppumpning.
|
Opgave 2: Datering af grundvand
 Den radioaktive isotop tritium 3H kan anvendes til datering af ungt vand, idet den har en kort halveringstid på ca. 12,5 år. Tritium blev tilført vandet via atomprøvesprængningerne i atmosfæren efter den anden verdenskrig. Den radioaktive isotop tritium 3H kan anvendes til datering af ungt vand, idet den har en kort halveringstid på ca. 12,5 år. Tritium blev tilført vandet via atomprøvesprængningerne i atmosfæren efter den anden verdenskrig.
- Hvis en atomprøvesprængning fandt sted i 1950, hvor stor en brøkdel af radioaktiviteten fra tritium var der så tilbage i 1975?
- Hvornår er der 10% af den oprindelige radioaktivitet tilbage?
Den radioaktive isotop kulstof-14 har en halveringstid på 5730 år. I teksten står der, at meget gammelt vand ikke indeholder radioaktivt kulstof-14. Strengt taget vil der dog altid være en lille smule, men mængden er så lille, at den ikke kan registreres
- Hvor mange gange er aktiviteten fra kulstof-14 blevet halveret, hvis der er tale om grundvand, der betegnes som værende meget gammelt vand?
- Hvis aktiviteten fra kulstof-14 var 100%, da grundvandet blev dannet, hvor mange procent er der så tilbage i dag?
|
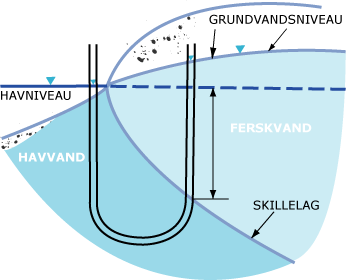
Opgave 3: Ferskvand flyder på saltvand
Betragt en vandsøjle og forklar, hvorfor tyngdekraften kan skrives ved
hvor ρ er densiteten, A er søjlens tværsnitsareal, h er søjlens højde, og g er tyngdeaccelerationen.
Tyngdekraften på en søjle ferskvand (i en boring inde på kysten) og en søjle saltvand (fra havet ned gennem sedimentet) er lige store ifølge princippet om forbundne kar (via det dybe saltvand i undergrunden). Ferskvandets densitet sættes til 1000 kg/m3, havvandets densitet sættes til 1025 kg/m3.
- Vis tommelfingerreglen, der siger, at ferskvandssøjlen er 1/40 højere end saltvandssøjlen.
- Grundvandsstanden i en boring vest for Holstebro er 2,1 m over havniveau. Hvor langt er der ned til saltvandsgrænsen?
Eksperiment
Vi kan selv udføre et forsøg med forbundne kar. Brug Databogen til at finde den præcise mængde salt, der skal opløses i vand for at saltindholdet (saliniteten) svarer til vesterhavsvand. Tommelfingerreglen ovenfor blev udledt for pæne værdier for densiteterne. Brug Databogen til at checke, om tommelfingerreglen også gælder i dette tilfælde.
Tag en gennemsigtig plastslange, fx 2 meter lang. Bøj den på midten og klem sammen, så der ikke er passage mellem rørene. Hæld ferskvand (vandhanevand) i det ene rør og saltvand i det andet rør. Vandstanden skal stå lige højt i hvert rør. Hvis røret er for tyndt, kan man få problemer med luftlommer, så vælg en passende rørdiameter.
Sammenklemningen løsnes, så de to kar med ferskvand og saltvand forbindes. Mål højdeforskellen og undersøg, om tommelfingerreglen holder.
|
|
Opgave 4: Isbjerge i havet
Populært sagt stikker et isbjerg 10 gange så langt under havoverfladen, som det stikker op over havoverfladen. Vi vil undersøge denne påstand teoretisk og eksperimentelt.
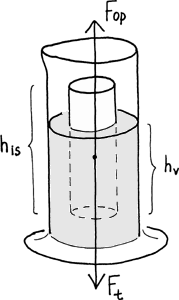 Ved frysepunktet er isens densitet 917 kg/m3. Hvis vi antager, at isbjerget er søjleformet, og at vandet er ferskvand med densitet 1000 kg/m3, kan vi ved at sammenligne tyngdekraften på vand- og issøjlerne beregne det teoretiske svar. Når det søjleformede isbjerg ligger stille i vandet, vil tyngdekraften på isen modsvares af opdriften. Archimedes lov siger, at opdriften er lige så stor, som tyngden af det vand, som isen fortrænger. Ved frysepunktet er isens densitet 917 kg/m3. Hvis vi antager, at isbjerget er søjleformet, og at vandet er ferskvand med densitet 1000 kg/m3, kan vi ved at sammenligne tyngdekraften på vand- og issøjlerne beregne det teoretiske svar. Når det søjleformede isbjerg ligger stille i vandet, vil tyngdekraften på isen modsvares af opdriften. Archimedes lov siger, at opdriften er lige så stor, som tyngden af det vand, som isen fortrænger.
|
Eksperiment
En plastslange på ca. 60 cm bøjes på midten og fyldes med vand. Slangen lægges i fryseren, og når vandet er frosset klemmes issøjlerne forsigtigt ud af slangen under rindende vand. En søjle anbringes i et højt, smalt måleglas med vand.
|
|
Opgave 5: 4 polsmålinger
Opgaven mangler pt.
|
|
Opgave 6: Bestemmelse af kornstørrelse
Kornstørrelsen af en sandprøve kan bestemmes på flere måder. Sandkorn med næsten ens diameter kan fremskaffes ved præcisionssigtning. Også flyvesand (fx fra Råbjerg Mile) vil bestå af næsten ens kornstørrelser. Tilsvarende vil det fine sand, der findes i mange tapeholdere, have en nogenlunde ensartet kornstørrelse – med en saks kan man let lave et fint hul til prøveudtagning, der så kan lukkes med tape bagefter. Endelig kan man skaffe sig en rimelig sandprøve fra sandkassen med to forskellige børnesier eller to forskellige stykker stof af passende maskestørrelse.
I det følgende skal vi gennemgå 4 metoder til bestemmelse af kornstørrelsen. Metoderne sammenlignes og de 4 resultater vurderes.
6a. Mikroskop
Hæld nogle sandkorn ud på mikroskopets glasplade. Vurdér den gennemsnitlige diameter og diameteren af de største korn, idet du sammenligner med mikroskopets lineal. Er der ingen skala på mikroskopet kan man sammenligne med et menneskehår (unge menneskers hovedhår er op til 0,1 mm, et hår fra armen ca. 0,05 mm), en fiskesnøre eller en kobbertråd. Trådens diameter kan bestemmes med en mikrometerskrue.
6b. Mikrometerskrue
En simpel metode til at bestemme sandkornenes omtrentlige størrelse er at placere 10-100 korn i målegabet på en mikrometerskrue.

Skrues mikrometerskruen forsigtigt i, indtil der kommer modstand, får man en værdi for de største korns diameter på den længste led – kornene vil i almindelighed være aflange.
Skrues der i til en let knasen – skrues ud – skrues i til en let knasen – skrues ud – skrues i til en let knasen, så vil man få en værdi for den typiske korndiameter.
Store korn kan dog måles enkeltvis.
6c. Sand gennem vand
Først lidt teori om Laminær strømning, når partikler bevæger sig gennem vand.
For et kugleformet korn i vand kan man vise, at tyngdekraften er givet ved formen
hvor r er kornets radius, ρ korn er kornets densitet, ρ vand er vands densitet, og g er tyngdeaccelerationen.
Man kan udnytte, at den laminære strømningsmodstand er givet ved kraften
hvor η er vands dynamiske viskositet, og vkorn er hastigheden, hvormed kornet synker i væsken. Når kornet daler med konstant hastighed er de to kræfter lige store, og man kan af de to udtryk vise, at kornets hastighed er givet ved
- Vis, at massen for et kugleformet korn er
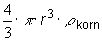
- Vis, at tyngdekraften på et kugleformet korn er
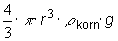
Archimedes’ lov siger, at opdriften på et nedsænket legeme er lig med tyngdekraften på den fortrængte vandmængde.
- Vis, at opdriften er
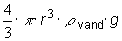
- Vis hermed, hvordan formel (1) fremkommer.
- Sæt de to udtryk for kraften lig hinanden, og vis hvordan formel (3) fremkommer.
Sandkorn defineres til at have en diameteren på 0,125 - 2 mm, og de mindre siltkorn har en diameter på 0,004 – 0,125 mm. Densiteten for sand sættes til 2700 kg/m3.
- Find i Databogen en værdi for vands dynamiske viskositet ved 10 °C, og bestem synkehastighederne i vand for hver af de tre nævnte diametre, der giver grænserne for sandkorn og siltkorn.
|
Eksperiment
I et cylinderglas med vand vil man kunne iagttage, hvordan sandpartiklerne synker. Brug en mørk baggrund for at få et godt billede. En fugtig fingerspids dyppes i sandprøven, og vandoverfladen berøres. Kornenes hastighed bestemmes simpelt med lineal og stopur. Fx kan man bestemme hastigheden for den tredje-hurtigste partikel og for midten af prøven.
Ved brug af formlen for hastigheden (3) kan man finde en værdi for kornenes radius.
|
6d. Vand gennem sand
Først lidt teori om Laminær strømning, når vand løber gennem porer.
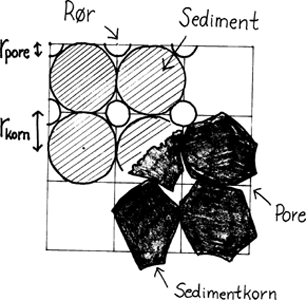
Når vand strømmer gennem porerne i sedimentet, taler vi om grundvand. I en simpel model for porernes beliggenhed tænker man på rækker af parallelle rør, hvor afstanden mellem rørene er givet ved den gennemsnitlige korndiameter. Rørets radius er porernes gennemsnitlige radius r pore, der i modellen kan sættes til en vis brøkdel af kornets gennemsnitlige radius r korn.
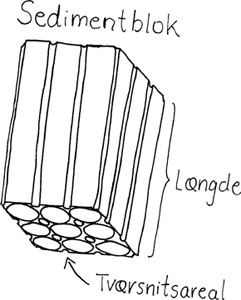
Vi antager, at rørene ligger som vist på tegningen, og at vi har en sedimentblok med længde L og tværsnitsareal A. Hver af de 9 kasser på figuren indeholder i alt ét helt rør. Da hver kasse har arealet (2·r korn)·( 2·r korn), fremgår det, at der i alt er
rør. Da hvert rør har et areal på 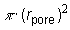 , bliver det samlede poreareal i modellen , bliver det samlede poreareal i modellen
Det er oplagt at forvente, at grundvandsstrømmen er laminær, når vandet siver gennem porerne. For en laminær strømning er den gennemsnitlige porehastighed i rørene givet ved formlen
h er vandhøjden over sedimentet og L er sedimentlagets tykkelse.
Vandmængden, der strømmer gennem sedimentet pr. tid, findes som produktet af de to udtryk.
Opgave: Swimmingpool
En 1,8 meter dyb swimmingpool er fyldt med vand til 10 cm fra kanten. Den ligger direkte på sedimentet (dvs. der er ingen støbt bund). Vi skal finde ud af, hvor hurtigt poolen tømmes, når vandet kan sive lodret ned i et 200 m tykt sedimentlag bestående af korn med diameteren henholdsvis 2 mm, 0,125 mm og 0,004 mm. Start med at betragte 1 m2 af poolen. Nedsivningen for denne m2 må foregå lige så hurtig som nedsivningen for hele poolen, da vandet siver lodret ned.
- Hvor stort et volumen (i kubikmeter) indeholder hver kvadratmeter af bassinet?
- Vi antager, at
 . Hvor stor bliver porernes areal på hver kvadratmeter af bassinet? . Hvor stor bliver porernes areal på hver kvadratmeter af bassinet?
- Af formel (5) fremgår det, at porehastigheden ændres med vandhøjden h. Imidlertid vil det tykke sedimentlag i praksis betyde, at faktoren
 i formlen ingen effekt får. Vis det! i formlen ingen effekt får. Vis det!
- Hvor stor bliver porehastigheden i hvert af de 3 tilfælde?
- Hvor stor bliver vandmængden, der strømmer gennem sedimentet pr. tid (dvs. hvor mange m3 vand løber der ud af hver m2 pool pr. sekund) i hvert af de 3 tilfælde?
- Hvor lang tid tager nedsivningen i hvert af de 3 tilfælde?
I forbindelse med poolen vil man sikkert være glad for en langsom nedsivning. Men andre steder prøver man på at gøre nedsivningen så hurtig som mulig. Det gælder bl.a. i forbindelse med omfangsdræn omkring huse med kælder. Hvis den fugtige jord støder direkte op til betonmuren, vil vandet ledes ind i kælderen, og er der ikke en god udluftning kommer kælderen til at lugte. Et drænrør graves ned hele vejen rundt uden om fundamentet. Røret graves ned til fundamentets underkant og tilsluttes kloakken, og et drænende materiale lægges i et bælte oven over røret. Herved sikres kælderens gode indeklima. Bæltet kan fx bestå af leca-nødder, der yderligere har den fordel, at de er luftholdige og derfor virker varme-isolerende på kælderen.
|
Eksperiment
 Nedsivning kan måles i et rør fyldt med vandmættet sand af en ensartet størrelse. Et fx 30 cm langt glas- eller gennemsigtigt plastrør lukkes med et stykke stof og en elastik i den nedre ende. Røret fyldes med sand til 6 cm fra toppen. Det er lettest at arbejde med tørt sand, der ikke klumper. Vand hældes i, og man checker om gennemstrømningen fungerer. Stoffets masker skal svare til rørets indhold – det skal holde sandet tilbage, samtidig med at det ikke må virke bremsende på vandgennemstrømningen i røret. Nedsivning kan måles i et rør fyldt med vandmættet sand af en ensartet størrelse. Et fx 30 cm langt glas- eller gennemsigtigt plastrør lukkes med et stykke stof og en elastik i den nedre ende. Røret fyldes med sand til 6 cm fra toppen. Det er lettest at arbejde med tørt sand, der ikke klumper. Vand hældes i, og man checker om gennemstrømningen fungerer. Stoffets masker skal svare til rørets indhold – det skal holde sandet tilbage, samtidig med at det ikke må virke bremsende på vandgennemstrømningen i røret.
Med en finger under bunden fyldes røret med vand. Med tusch-mærker ved 1 cm og 5 cm og et stopur kan man fjerne fingeren og starte forsøget. Hastigheden voverflade, hvormed vandoverfladen falder, kan nu bestemmes.
Vandet løber ikke ud med samme hastighed, øverst går det hurtigst, nederst går det langsomst. Den hastighed vi måler, svarer i gennemsnit til en 3 cm vandsøjle. Sandsøjlen er 24 cm.
Har vandslangen arealet A, og falder vandoverfladen med hastigheden voverflade, giver produktet af de to størrelser den mængde vand, der ledes gennem slangen pr. sekund.
Hvis vi igen antager, at  , kan vi beregne porernes areal i vandslangen fra (4). Heraf følger porehastigheden vpore, da vandmængden, der strømmer gennem et tværsnit af slangen pr. tid, er den samme, om man lægger snittet oppe i vandet eller nede i sandet. , kan vi beregne porernes areal i vandslangen fra (4). Heraf følger porehastigheden vpore, da vandmængden, der strømmer gennem et tværsnit af slangen pr. tid, er den samme, om man lægger snittet oppe i vandet eller nede i sandet.
Endeligt kan man med (5) bestemme r pore og med antagelsen r korn.
|
|
Demonstration
Forskellen på de to hastigheder vpore og vslange kan vises med frugtfarve. Drypper man nogle dråber frugtfarve i vandet under synkeeksperimentet ovenfor, kan man følge farven med gennem slangen. Når farven når ned i sandet, iagttages et tydeligt hastighedsskift.
|
|
|
Opgave 7: Turbulent strømning
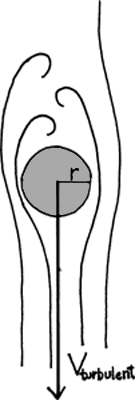 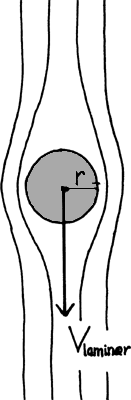 Når et sandkorn synker ned gennem vand, vil vandet strømme rundt om sandkornet. Ved lave hastigheder vil vandet strømme laminært, men når hastigheden øges (hvis kornet bliver større), vil strømningen på et tidspunkt gå fra at være laminær til at blive turbulent. Reynolds-tallet Re kan bruges til at afgøre strømningens type. Det defineres i dette tilfælde som Når et sandkorn synker ned gennem vand, vil vandet strømme rundt om sandkornet. Ved lave hastigheder vil vandet strømme laminært, men når hastigheden øges (hvis kornet bliver større), vil strømningen på et tidspunkt gå fra at være laminær til at blive turbulent. Reynolds-tallet Re kan bruges til at afgøre strømningens type. Det defineres i dette tilfælde som
r er kornets radius, v korn er synkehastigheden for kornet, ρ vand er vands densitet, og η er vands dynamiske viskositet. Når hastigheden bliver så stor, at Reynolds-tallet overstiger 1 bliver strømningen turbulent.
For et dalende, kugleformet korn i vand kan man vise, at tyngden på kornet modsvares af en turbulent strømningsmodstand. Ifølge teorien gælder
hvor ρkorn er kornets densitet, ρvand er vands densitet, g er tyngdeaccelerationen, og A er tværsnitsarealet af det dalende sandkorn.
Herfra kan man vise, at den turbulente synkehastighed for et korn bliver
- Udled formlen for synkehastigheden.
- Vis, at formlen for synkehastigheden i tilfældet med sand, der har ρ korn = 2700 kg/m3, reduceres til
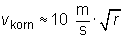 , idet radius angives i meter. , idet radius angives i meter.
Eksperiment
 Eksperimentelt kan man undersøge, om store dalende sandkorn synker laminelt eller turbulent (dvs. om Reynolds-tallet er under eller over 1). Med lineal og stopur kan vi let finde synkehastigheden v korn. Brug et langt cylinderglas eller en lang gennemsigtig plasticslange (1-2 meter), samt en lineal og et ur til at bestemme v korn. Bemærk, at kornene kan trække en luftboble med ned. Problemet undgås ved at fugte kornene før de slippes. Til opstillingen kan det være en fordel med ovenbelysning af slangen på en mørk baggrund for at se sandkornene. Vi kan måle de store sandkorns radius r med en mikrometerskrue – vi antager, at kornene er kugleformede, selvom det langtfra altid er tilfældet. Dermed kan vi finde Re ud fra formlen. Eksperimentelt kan man undersøge, om store dalende sandkorn synker laminelt eller turbulent (dvs. om Reynolds-tallet er under eller over 1). Med lineal og stopur kan vi let finde synkehastigheden v korn. Brug et langt cylinderglas eller en lang gennemsigtig plasticslange (1-2 meter), samt en lineal og et ur til at bestemme v korn. Bemærk, at kornene kan trække en luftboble med ned. Problemet undgås ved at fugte kornene før de slippes. Til opstillingen kan det være en fordel med ovenbelysning af slangen på en mørk baggrund for at se sandkornene. Vi kan måle de store sandkorns radius r med en mikrometerskrue – vi antager, at kornene er kugleformede, selvom det langtfra altid er tilfældet. Dermed kan vi finde Re ud fra formlen.
Gentages eksperimentet med et blyhagl, kan man checke, at Re >1.
Find den reducerede formel for synkehastigheden for bly (som du fandt den for vand).
Vis, at synkehastigheden for bly er proportional med  ved at lave en måleserie med mange forskellige størrelser blyhagl. Sammenlign proportionalitetsfaktoren med teorien. ved at lave en måleserie med mange forskellige størrelser blyhagl. Sammenlign proportionalitetsfaktoren med teorien.
|
|
|
Opgave 8: Vandstrømning i slange
Når vand strømmer gennem et rør eller en slange, kan det løbe på to forskellige måder. Ved lave hastigheder vil vandet løbe laminært: Vandmolekylerne løber parallelt gennem røret, og hvor røret ender, ses en rolig stråle. Øges hastigheden, vil strømningen ved et punkt ændre karakter og herefter blive turbulent: Strømhvirvler blander vandet i røret, og ved mundingen ses en urolig stråle.
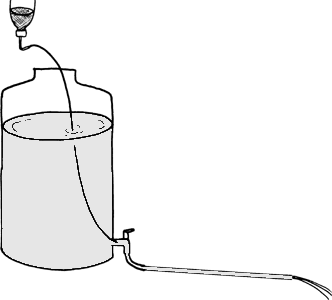
Omslaget kan demonstreres med en vandfyldt beholder, der tømmes gennem en slange. Er rørets dimensioner valgt korrekt, vil den turbulente strømning erstattes af en laminær, når vandstanden kommer under et vist punkt. Tilsætter man lidt farvestof i slangen (fx rødbedesaft), fremgår det tydeligt, at den turbulente strømning blander saften ud i hele røret, mens saften i det laminære tilfælde blot bliver en tynd streg gennem røret.
Eksperiment
Vi vil undersøge de to typer strømning og finde omslagspunktet mellem laminær og turbulent strømning mere præcist.
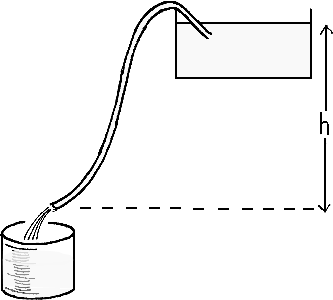 Eksperimentet kan gennemføres med en opstilling med vandkar, plastslange (som vist på figuren) og et måleglas. For varierende højdeforskelle mellem vandstanden i karret og slangens udløbsniveau – svarende til forskellige vandhastigheder – måles den tid, det tager at fylde måleglasset. Slangens dimensioner og måleglassets rumfang noteres også. Eksperimentet kan gennemføres med en opstilling med vandkar, plastslange (som vist på figuren) og et måleglas. For varierende højdeforskelle mellem vandstanden i karret og slangens udløbsniveau – svarende til forskellige vandhastigheder – måles den tid, det tager at fylde måleglasset. Slangens dimensioner og måleglassets rumfang noteres også.
Fra formlen rumfang = tværsnitsareal · længde kan længden af den vandslange, der skal til for at fylde måleglasset, beregnes. Endeligt kan vi med formen længde = hastighed · tid beregne strømningshastigheden. Udregningerne kan med fordel foretages med lommeregnerens lister.
Til at illustrere hvordan strømningshastigheden ændrer sig med højdeforskellen, laves en (Δh, v)-graf.
Ved små højdeforskelle strømmer vandet laminært, ved store højdeforskelle strømmer det turbulent. Ud fra brøken  har fysikeren O. Reynolds fundet at omslagsområdet mellem de to strømninger kan beregnes til at være mellem 1 og 1,3. Her er r rørets radius, Δh er højdeforskellen og L er rørets længde (alle størrelser er angivet i mm). har fysikeren O. Reynolds fundet at omslagsområdet mellem de to strømninger kan beregnes til at være mellem 1 og 1,3. Her er r rørets radius, Δh er højdeforskellen og L er rørets længde (alle størrelser er angivet i mm).
Brug Reynolds værdi til at beregne i hvilket højdeinterval, du vil forvente at finde omslaget for din slange. Stemmer det med dine målinger?
Ifølge teorien gælder at v og h er proportionale for laminært strømmende vand, og at v2 og h er proportionale for turbulent strømmende vand. Stemmer dette med din figur? Lav én regression, der passer til den første del af målepunkterne, og én anden regression, der passer til den anden del af målepunkterne.
Årsagen til at kurven knækker, når strømningen går over til at være turbulent, er, at modstanden i slangen øges. For os synes det måske uvæsentligt (vi sænker bare mundingen yderligere og sætter endnu mere fart på vandet), men for vandværkerne betyder det, at pumperne skal yde meget mere, hvis hastigheden bliver så stor, at vandet begynder at turbulere i rørene. Derfor tager man hensyn til det forventede vandforbrug, når man dimensionerer rørene fra vandværket til forbrugerne.
|
|
Eksperiment
 Hvor stort er vandtrykket i vandhanen? Hvor stort er vandtrykket i vandhanen?
Med en haveslange og en høj flagstang, kan vi måle trykket i vandhanen. Slangen hejses op til der ikke kommer mere vand ud. Vandtrykket angives i meter-vandsøjle. Er flagstangen ikke høj nok, finder vi at trykket er større end en vis værdi.
Fra formlen p = ρ · g · h kan trykket p findes i pascal (SI-enheden for tryk). Trykket han sammenlignes med den værdi, vi måler med en trykmåler.
|
|
Opgave 9: Værket ved Regnemark
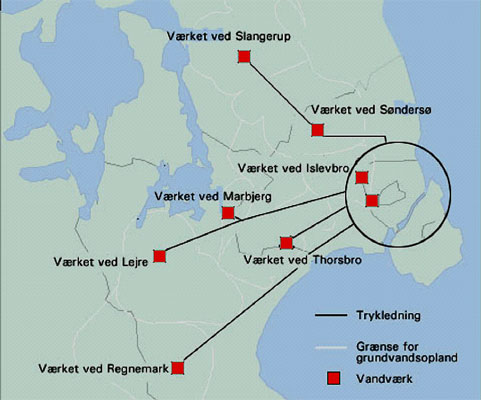
Københavns Energi
Københavns Energi indvinder ca. 65 mio. m³ grundvand årligt til fremstilling af drikkevand. Udover at stå for vandforsyningen i Københavns Kommune leverer det vand til 19 andre kommuner i hovedstadsområdet. Vandet indvindes i et område, der strækker sig fra Ringsted i syd til Arresø i nord.
REGNEMARK, opført 1960-1964
(tal i parantes er søvand)
|
Antal boringer
|
121
|
|
Indvindingstilladelse
|
16,00 (15,00) mio. m3
|
|
Ydeevne
|
15,00 (7,00) mio. m3
|
|
Indvinding
|
14,34 (1,75) mio. m3
|
|
Produktion
|
14,02 (1,31) mio. m3
|
|
Energiforbrug
|
4.087,86 MWh
|
|
Energiforbrug pr.100 m3
|
26,67 kWh
|
|
Energipris pr.100 m3
|
14,82 kr.
|
|
- Københavns Energi leverer drikkevand af høj kvalitet. Gennem daglige kontroller sikres det, at vandkvaliteten altid er i top.
- Kvaliteten af det leverede vand er god og overholder de gældende krav.
- Vandet er generelt forholdsvis hårdt (18-25 °dH). Hårdhedsgraden er et udtryk for mængden af opløst kalk i vandet. Årsagen til det hårde vand er, at vandet primært indvindes fra kalklag i undergrunden.
- Hårdt vand kan i visse tilfælde give problemer med kalkudfældning, fx i kedler, vaskemaskiner mv. Samtidig kan der være behov for at øge doseringen af vaskepulver ved tøjvask.
- Da hovedparten af det producerede vand stammer fra velbeskyttet grundvand, er vandet biologisk stabilt og giver ikke anledning til uønsket bakterievækst i rørledningerne.
- På et af vandværkerne, Værket ved Regnemark, tilsættes dog små mængder monokloramin til vandet for at sikre en stabil bakteriologisk kvalitet, da værket periodevist bruger søvand til vandproduktion. Dette kan give anledning til en kloragtig smag i visse dele af København.
- Eventuel klorsmag kan fjernes ved at stille vandet i køleskab et par timer, før det drikkes.
Rørledningen fra Værket ved Regnemark til København er 38 km og har en diameter på 1,2 m .
- Beregn omslagsområdet mellem laminær og turbulent strømning i dette rør.
Når pumperne kører for fuld kraft, leverer de en trykstigning på 112 meter-vandsøjle. Man skal dog huske på, at der er en højdeforskel mellem vandværket i Regnemark og vandoverfladen i Kbh,s højeste vandreservoir ( 50,1 m over havniveau).
- Hvilken type strømning er der i røret?
Med en graf for dagsvariationen i timeforbruget hos Københavns vandforsyning, kan du tælle tern og bestemme det samlede vandforbrug i Storkøbenhavn. Med data for højdebeholdernes størrelse i København (309.000 m3), kan du beregne, hvor lang tid, der er reserver til et normalt forbrug – forudsat at der ikke tilføres nyt vand fra Regnemark (driftsstop!).
Kommer pumperne i gang igen efter at højdebeholderne er helt tømte, kan du beregne, hvor lang tid det tager, før de er fyldte igen.
|
 Den radioaktive isotop tritium 3H kan anvendes til datering af ungt vand, idet den har en kort halveringstid på ca. 12,5 år. Tritium blev tilført vandet via atomprøvesprængningerne i atmosfæren efter den anden verdenskrig.
Den radioaktive isotop tritium 3H kan anvendes til datering af ungt vand, idet den har en kort halveringstid på ca. 12,5 år. Tritium blev tilført vandet via atomprøvesprængningerne i atmosfæren efter den anden verdenskrig.
 Ved frysepunktet er isens densitet 917 kg/m3. Hvis vi antager, at isbjerget er søjleformet, og at vandet er ferskvand med densitet 1000 kg/m3, kan vi ved at sammenligne tyngdekraften på vand- og issøjlerne beregne det teoretiske svar. Når det søjleformede isbjerg ligger stille i vandet, vil tyngdekraften på isen modsvares af opdriften. Archimedes lov siger, at opdriften er lige så stor, som tyngden af det vand, som isen fortrænger.
Ved frysepunktet er isens densitet 917 kg/m3. Hvis vi antager, at isbjerget er søjleformet, og at vandet er ferskvand med densitet 1000 kg/m3, kan vi ved at sammenligne tyngdekraften på vand- og issøjlerne beregne det teoretiske svar. Når det søjleformede isbjerg ligger stille i vandet, vil tyngdekraften på isen modsvares af opdriften. Archimedes lov siger, at opdriften er lige så stor, som tyngden af det vand, som isen fortrænger.







 Nedsivning kan måles i et rør fyldt med vandmættet sand af en ensartet størrelse. Et fx 30 cm langt glas- eller gennemsigtigt plastrør lukkes med et stykke stof og en elastik i den nedre ende. Røret fyldes med sand til 6 cm fra toppen. Det er lettest at arbejde med tørt sand, der ikke klumper. Vand hældes i, og man checker om gennemstrømningen fungerer. Stoffets masker skal svare til rørets indhold – det skal holde sandet tilbage, samtidig med at det ikke må virke bremsende på vandgennemstrømningen i røret.
Nedsivning kan måles i et rør fyldt med vandmættet sand af en ensartet størrelse. Et fx 30 cm langt glas- eller gennemsigtigt plastrør lukkes med et stykke stof og en elastik i den nedre ende. Røret fyldes med sand til 6 cm fra toppen. Det er lettest at arbejde med tørt sand, der ikke klumper. Vand hældes i, og man checker om gennemstrømningen fungerer. Stoffets masker skal svare til rørets indhold – det skal holde sandet tilbage, samtidig med at det ikke må virke bremsende på vandgennemstrømningen i røret.
 Når et sandkorn synker ned gennem vand, vil vandet strømme rundt om sandkornet. Ved lave hastigheder vil vandet strømme laminært, men når hastigheden øges (hvis kornet bliver større), vil strømningen på et tidspunkt gå fra at være laminær til at blive turbulent. Reynolds-tallet Re kan bruges til at afgøre strømningens type. Det defineres i dette tilfælde som
Når et sandkorn synker ned gennem vand, vil vandet strømme rundt om sandkornet. Ved lave hastigheder vil vandet strømme laminært, men når hastigheden øges (hvis kornet bliver større), vil strømningen på et tidspunkt gå fra at være laminær til at blive turbulent. Reynolds-tallet Re kan bruges til at afgøre strømningens type. Det defineres i dette tilfælde som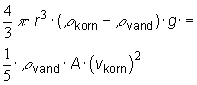
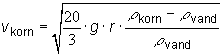
 Eksperimentelt kan man undersøge, om store dalende sandkorn synker laminelt eller turbulent (dvs. om Reynolds-tallet er under eller over 1). Med lineal og stopur kan vi let finde synkehastigheden v korn. Brug et langt cylinderglas eller en lang gennemsigtig plasticslange (1-2 meter), samt en lineal og et ur til at bestemme v korn. Bemærk, at kornene kan trække en luftboble med ned. Problemet undgås ved at fugte kornene før de slippes. Til opstillingen kan det være en fordel med ovenbelysning af slangen på en mørk baggrund for at se sandkornene. Vi kan måle de store sandkorns radius r med en mikrometerskrue – vi antager, at kornene er kugleformede, selvom det langtfra altid er tilfældet. Dermed kan vi finde Re ud fra formlen.
Eksperimentelt kan man undersøge, om store dalende sandkorn synker laminelt eller turbulent (dvs. om Reynolds-tallet er under eller over 1). Med lineal og stopur kan vi let finde synkehastigheden v korn. Brug et langt cylinderglas eller en lang gennemsigtig plasticslange (1-2 meter), samt en lineal og et ur til at bestemme v korn. Bemærk, at kornene kan trække en luftboble med ned. Problemet undgås ved at fugte kornene før de slippes. Til opstillingen kan det være en fordel med ovenbelysning af slangen på en mørk baggrund for at se sandkornene. Vi kan måle de store sandkorns radius r med en mikrometerskrue – vi antager, at kornene er kugleformede, selvom det langtfra altid er tilfældet. Dermed kan vi finde Re ud fra formlen.
 Eksperimentet kan gennemføres med en opstilling med vandkar, plastslange (som vist på figuren) og et måleglas. For varierende højdeforskelle mellem vandstanden i karret og slangens udløbsniveau – svarende til forskellige vandhastigheder – måles den tid, det tager at fylde måleglasset. Slangens dimensioner og måleglassets rumfang noteres også.
Eksperimentet kan gennemføres med en opstilling med vandkar, plastslange (som vist på figuren) og et måleglas. For varierende højdeforskelle mellem vandstanden i karret og slangens udløbsniveau – svarende til forskellige vandhastigheder – måles den tid, det tager at fylde måleglasset. Slangens dimensioner og måleglassets rumfang noteres også. Hvor stort er vandtrykket i vandhanen?
Hvor stort er vandtrykket i vandhanen?