Opgave E.04: Astrometri med VLT som interferometer

Nøjagtig bestemmelse af en stjernes position på himlen kaldes astrometri. Ved at anvende VLT som interferometer vil man få mulighed for at lave astrometri med hidtil uhørt nøjagtighed.

Et vigtigt mål for disse interferometriske målinger er de stjerner, hvor man med radialhastighedsmålinger har fundet planeter, se opgave E.01 - opgave E.03. I modsætning til målingerne baseret på radialhastigheder (opgave E.02), giver astrometri mulighed for at bestemme massen for en evt. planet.

Med VLT som interferometer regner man med at kunne bestemme en stjernes position med en nøjagtighed på 10 · 10^-6 buesekund. Dette er grænsen for det opnåelige for målinger på jorden op igennem atmosfæren. Måske kan det vise sig at være for optimistisk, og i første omgang stiller man sig da også tilfreds med 50 ·10^-6 buesekund.

Denne nøjagtighed kan dog kun opnås ved måling af vinkelafstanden mellem to stjerner, som ligger tæt på hinanden. Hvis den ene stjerne ligger stille, mens den anden bevæger sig på grund af en planet, kan denne bevægelse måles med denne meget store nøjagtighed.

På figuren ses, hvordan man i afstanden 10 pc ville kunne se Solens bevægelse. Bevægelsen skyldes primært planeten Jupiter.

Der gælder, at 1 buesekund = 1¢¢ =

og at 1 pc = 3,086 · 10¹⁶ m.

Solens radius er 6,96 · 10⁸ m.

På figuren er afsat enheden 0,001¢¢. Omregn 0,001¢¢ til radianer. Hvor stor en afstand svarer det til i afstanden 10 pc? Giv resultatet i km.
Hvor mange buesekunder er Solens radius i afstanden 10 pc. Indtegn Solen som en skive på figuren.

En astronaut kører en tur på Månen i sin månebil. Med VLT måler vi afstanden mellem bilens to forlygter - nøjagtigheden er 50ž10^-6 buesekund. Afstanden til Månen er ca. 3,8 ž10⁸ m.

Hvor god er nøjagtigheden (i meter) i denne måling?

En stjerne med en planet befinder sig i afstanden 10 pc. På grund af planeten gennemfører stjernen en cirkelbevægelse på himlen. For med sikkerhed at kunne se denne cirkelbevægelse, skal dens vinkelradius være ca. 5 gange større end nøjagtigheden.

Radius i cirkelbevægelsen skal altså svare til 5 gange 50 · 10^-6 buesekund. Beregn den nødvendige radius i cirkelbevægelsen. Giv resultatet i km.
Se på ovenstående figur. Vil det være muligt for fremmede væsner i afstanden 10 pc at se Solens bevægelse på grund af Jupiter? Vi forudsætter at de råder over udstyr der er lige så godt som VLT!

Ved hjælp af Keplers love og lidt geometri kan man vise at en planets cirkelbevægelse omkring en stjerne vil få denne til bevæge sig med en vinkel-“radius”, målt i buesekunder, på himlen givet ved:

vinkelradius = 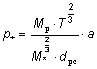(4)

Hvor M_p og M_* er masserne for planet og stjerne, målt i antal solmasser.

T er planetens omløbstid i år. d er afstanden til stjernen målt i parsec.

Indsæt værdier for Jupiters bevægelse omkring Solen og sammenlign med ovenstående figur. (d = 10 pc. M_Jupiter = 1,9ž10²⁷ kg. M_Sol = 1,99ž10³⁰ kg)
Indsæt også værdier for Jordens masse, M_Jorden = 5,98ž10²⁴ kg, og omløbstid. Kan VLT se en stjerne som Solen i afstanden 10 pc bevæge sig på grund af en planet som Jorden?

Som det fremgår af opgave E.02, giver måling af radialhastigheder kun mulighed for at finde en nedre grænse for planetens masse.

Lad os antage, at VLT engang i år 2001 måler på planetsystemet 47 Ursae Majoris og finder, at stjernen bevæger sig i en cirkelbane med en "vinkelradius” på 0,60 ž10^-3buesekund. Afstanden til 47 Ursae Majoris er 14,4 pc.

Brug dette samt oplysningerne i Opgave E.02 til at finde massen for planeten omkring 47 Ursae Majoris. Husk de lidt underlige enheder, der anvendes i formel (4).
Brug, at M_planetžsin(i) = 2,41ž M_Jupiter : Med hvilken vinkel hælder planetens bane i forhold til sigtelinien?

For nylig (vinteren 1999) har astronomer annonceret opdagelsen af hele tre planeter omkring stjernen Ypsilon Andromedae.

For dette planetsystem gælder at:

d = 13,47 pc. M_* = 1,3 solmasser.

Planeternes omløbstider: T_a = 4,617 døgn, T_b = 241,2 døgn, T_c = 1267 døgn

Mindste værdier for planeternes masser: M_a = 0,71, M_b = 2,11, M_c = 4,61

Vil det være muligt at se Ypsilon Andromedae bevæge sig på grund af én eller flere af disse planeter?