Opgave E.03: Cirkel- og ellipsebaner på himlen
På instruct1.cit.cornell.edu/courses/astro101/java/binary/binary.htm kan du finde en animation, der viser, hvordan to stjerner bevæger sig omkring hinanden. Vi vil bruge animationen til at undersøge radialhastighedskurverne for nogle af de kendte stjerner med planeter.
-
Hent animationen
Klik på ovenstående URL for at hente den ønskede animation. Lad animationen køre og find de dele, der vises:
- banebevægelsen set fra oven
- banebevægelsen set i retningen fra Jorden
- spektrallinierne
- radialhastighedskurverne
- ”skydere” til regulering af bane-parametre
Man kan ændre på følgende parametre:
- M1 og M2: Masserne for de to stjerner
- a: Den halve storakse (radius for en cirkelbevægelsen)
- e: Excentriciteten af ellipsebanen (e = 0 for en cirkelbane)
- i: Inklinationen.
- w: Storaksens vinkel i forhold til synslinien
- Simulerings-hastigheden
I kassen Priviliged view ses banen altid fra oven, mens kassen Earth view viser stjernernes baner, som de ses fra Jorden.
Ændringer i bane-parametrene får virkning, når du klikker på Enter.
-
Radialhastighedskurver
Sammenlign de to radialhastighedskurver. Hvilke forskelle og ligheder er der imellem de to kurver? Prøv at ændre massen for en af stjernerne, hvad sker der med radialhastighedskurverne?
Brug formlen (se (4) i opgave E.02)
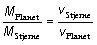
og forklar, at de to radialhastighedskurver er ligedannede.
-
Cirkelbaner. Sæt e = 0
Hvilken betydning har masserne for banebevægelsen, hvordan ser banerne ud i tilfældet Solen og Jupiter. Sæt M1 = 1000, da MSol » 1000 ž MJupiter. Justér også simulationshastigheden.
Den ene radialhastighedskurve er tydeligvis en sinuskurve. Gør rede for, at det samme må være tilfældet med den anden kurve. Hvilken af de to kurver kan astronomerne se?
Hvorfor er det ikke helt rigtigt, at planeten bevæger sig i en bane omkring stjernen? Dette bliver helt tydeligt, når M1 » M2.
Hvilken betydning har inklinationen for radialhastighedskurven for stjernen?
Ofte er planeternes baner langt fra at være cirkelbaner, men er i stedet ellipsebaner, jf. Keplers love
-
Betydningen af excentriciteten. Fasthold M1, M2, a. Sæt i = 90 og w = 0.
Undersøg hvordan radialhastighedskurverne afhænger af excentriciteten. Sammenlign med kurverne for Gliese 876 og for HD168443 - for hvilken er excentriciteten størst, hvordan ses det på radialhastighedskurverne?
I hvilken del af ellipsebanen er hastigheden størst?
For HD168443 vender spidserne nedad, for Gliese 876 er det omvendt. Hvad fortæller det om planetbanerne?
Se omhyggeligt på radialhastighedskurven for 47 Ursae Majoris. Hvordan kan man se på kurven, at banen faktisk ikke er helt cirkelformet - excentriciteten er 0,09?
-
Retningen i forhold til synslinien, w. Sæt f.eks. e = 0,6.
Undersøg, hvordan radialhastighedskurven afhænger af synslinievinklen, w.
Sammenlign med kurven for 16 Cygni B, prøv at finde ud af, hvor stor w er for planetbanen omkring denne stjerne.
Gå evt. til cannon.sfsu.edu/~gmarcy/planetsearch/7504/7504.html og se nærmere på denne meget specielle planet. Sammenlign f.eks. med planetbanerne for solsystemet, prøv at regne lidt på temperaturforholdene på planeten.
Radialhastighedskurve for HD168443: