Opgave E.02: Opdagelsen af exoplaneter - radialhastigheder

Vi så i opgave E.01, at man kan finde radialhastigheden for en stjerne ved at måle dopplerforskydningen af lyset fra stjernen. Denne teknik har man brugt til at finde stjerner, hvor en planet er i kredsløb om stjernen ganske som Jorden og de andre planeter omkring Solen.

Planeten bevæger sig ifølge Keplers love i en ellipsebane omkring stjernen påvirket af gravitationskraften fra stjernen. Da planeten i følge Newtons 3. lov også påvirker stjernen med en kraft, vil også stjernen bevæge sig i en ellipsebane.

Set fra Jorden giver det anledning til en varierende radialhastighed for stjernen, som astronomerne kan måle.

På figuren ses en måling af radialhastigheder for stjernen 47 Ursae Majoris, hvor en planet er i omløb - næsten i en cirkelbane. Omløbstiden for stjernen - og den omkredsende planet - er bestemt til 1094 dage.

Til dato (juli 1999) har man fundet i alt 20 exoplaneter, se f.eks.:

cannon.sfsu.edu/~gmarcy/planetsearch/doppler_table.html

Mens dette skrives, annoncerer ESO opdagelsen af en exoplanet omkring stjernen iota Horologii. Se: http://www.eso.org/outreach/press-rel/pr-1999/pr-12-99.html. Dette er ESO’s første opdagelse på dette felt, der er i rivende udvikling!

Kontrollér på figuren, at omløbstiden er: T = 1094 dage.
Antag at stjernen bevæger sig i en cirkelbane, der ses ”fra kanten”. Forklar at radialhastighedens variation kan beskrives ved en sinuskurve. Hvordan aflæses på figuren, at stjernens hastighed i cirkelbanen er 47,7 m/s?

Radialhastighedskurve for stjernen 47 Ursae Majoris

Se: cannon.sfsu.edu/~gmarcy/planetsearch/47UMa/47UMa.html

Forklaring på de følgende formler (1) - (3) kræver kendskab til gravitationsloven svarende til fysik højt niveau. Se evt. opgave E.05

I følge en af Keplers love er planetens afstand, a, til stjernen bestemt ved formlen:

(1)

er gravitationskonstanten og M_stjerne er stjernens masse.

Massen af 47 Ursae Majoris kan tilnærmelsesvis bestemmes ved at se på fordelingen af bølgelængder i lyset fra stjernen og sammenligne med lyset fra Solen.

Man ved således, at 47 Ursae Majoris vejer ca. 1 solmasse. M_sol = 1,99 · 10³⁰ kg.

Beregn afstanden fra 47 Ursae Majoris til planeten.

Planetens hastighed i cirkelbanen er givet ved:

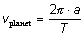(2)

Forklar formlen og beregn planetens hastighed i banen rundt om 47 Ursae Majoris.

Formel (2) gælder kun for en planet i en cirkelbane. For ellipsebaner gælder generelt at:

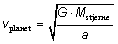(3)

Beregn planetens hastighed med formel (3) og sammenlign med resultatet fra (2).

Endelig gælder formlen:

(4)

Iflg. figuren er v_stjerne = 47,7 m/s.

Beregn planets masse i kg. Omregn planetens masse til antal Jupiter-masser, idet M_Jup.= 1,90 · 10²⁷ kg.

Beregningen i e. forudsætter, at vi ser planetens bane lige fra kanten. Hvis banen i virkeligheden hælder vinklen i (= ”inklinationen”) i forhold til himmelplanen gælder at

v_stjerne žsin( i ) = 47,7 m/s.

Brug den viste figur til at forklare faktoren sin(i).
Gør rede for, at den i e. beregnede størrelse ikke er planetens masse, men i stedet

M_planet · sin( i ).

Find planetens masse i tilfældet, hvor i = 45°.

Normalt kender man ikke inklinationen i, og måling af radialhastigheder kan derfor ikke bruges til at bestemme massen af planeten. Metoden giver kun en nedre grænse for planetens masse.

For nogle stjerner kendes inklinationen af stjernens rotation om sin egen akse med nogenlunde sikkerhed. Hvis man forudsætter, at planeten roterer i samme plan, fås en omtrentlig værdi for inklinationen af planetens baneplan.

Andre radialhastighedskurver kan ses her:

cannon.sfsu.edu/~gmarcy/planetsearch/doppler.html

Hvis du vil se nogle af stjernerne med egne øjne, er her en vejledning:

cfa-www.harvard.edu/afoe/they-are-everywhere.gif

Et andet bud på et stjernekort til dette er: