Opgave E.05: Gravitationsloven for stjerne og planet
Opgaven handler om gravitationsloven og forudsætter fysik på højt niveau.
Vi ser på et system bestående af en stjerne og en planet, hvor de begge bevæger sig i en jævn cirkelbevægelse påvirket af hinandens tyngdekraft, jf. opgave E.03 c.
Med figurens betegnelser gælder at:
 og og  (1) (1)
hvor T er perioden i de to cirkelbevægelser.
-
Vis at de to formler i (1) giver:
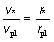 (2) (2)
Kraften i cirkelbevægelserne er givet ved gravitationsloven:
 (3) (3)
Hvor m* og mpl er masserne for stjerne og planet.
Da gælder:
 (4) (4)
-
Gør rede for, at (4) giver:
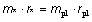 ( 5) ( 5)
-
Og gør rede for, at ligningerne (2) og (5) giver:
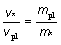 (6) (6)
Dette er ligning (4) i opgave E.02
-
Hvad gælder der om impulserne for planet og stjerne?
Beskrivelsen af planetens og stjernens bevægelse i opgave E.02 er ikke helt korrekt. Planeten roterer ikke omkring stjernen, men bevæger sig lige som stjerne i en cirkelbane omkring det fælles tyngdepunkt.
Det betyder, at formlen 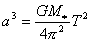 i opgave E.02 i opgave E.02
skal erstattes af (se opgave g.):
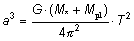 (7) (7)
hvor a = ro + r Pl er afstanden fra stjerne til planet.
Da planetens har en væsentlig mindre masse end stjernen, bliver fejlen i beregning af a ikke ret stor.
-
Brug tallene for 47 Ursae Majoris og find fejlens størrelse i procent.
-
Hvor stor skal planetens masse være i forhold til stjernen for at give en fejl i a på 1% ?
Formlen (7) kan vises således:
-
Isolér r i (5) og indsæt udtrykket i formlen for a. Isolér nu rpl og vis at
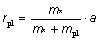
-
Indsæt denne formel for rpl i formlen 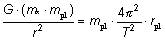 fra (4). Vis nu formel (7). fra (4). Vis nu formel (7).
|