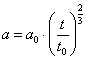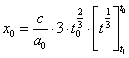|
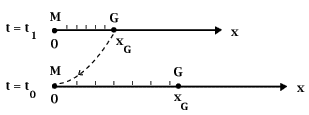
Opgave 21: Forskellige afstandsmåli Einstein-de Sitter modellen Vi vil nu beregne de samme tre afstande som i opgave 20, hvor z = 4, blot nu under den forudsætning, at universet udvider sig efter Einstein-de Sitter modellen, I denne model sker der en langsom opbremsning af udvidelseshastigheden, og rummet er helt fladt – ikke krumt.
Man kan vise, at afstanden til galaksen ved lysmodtagelsen er givet ved:
Sammenlign resultaterne for de tre afstande i denne opgave med resultaterne fra opgave 20. Bemærk, at svarene afhænger væsentligt af valget af model for universets udvidelse. Forskerne er endnu ikke i stand til med sikkerhed at vælge den rigtige model – Einstein-de Sitter er blot et „bedste gæt"!
|