Opgave 20: Forskellige afstandsmål

– udvidelse med konstant hastighed

Denne opgave handler om en fjern galakse med en rødforskydning på z = 4.

Vi må derfor regne med, at universet har udvidet sig, mens lyset har været undervejs til Mælkevejen. Vi vil nu beregne afstanden til galaksen.

Hertil vælger vi en meget simpel kosmologisk model, hvor universet kan sammenlignes med overfladen af en ballon, der bliver pustet op.

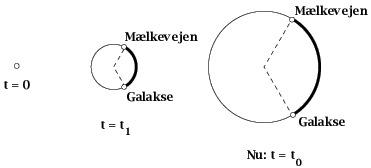
Vi går desuden ud fra, at rummets udvidelseshastighed har været konstant indtil i dag, hvor „radius" er 10 mia. lysår. Se figuren.

1. Lyset er rødforskudt med z = 4. Hvor mange gange større er universet blevet, siden lyset blev udsendt? Brug svaret til at finde universets = ballonens „radius", da lyset blev udsendt.

Brug at t₀ = 15 · 10⁹ år. Dette er Hubbletiden fra opgave 3 med

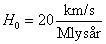
(hvor vi netop regnede med en konstant udvidelseshastighed).

2. Beregn nu udvidelseshastigheden af universets „radius" (i brøkdel af lyshastigheden c). Brug resultatet til at beregne universets alder, da lyset blev udsendt.

3. Hvilken afstand har lyset fra galaksen faktisk bevæget sig?

Vi vil nu se på galaksens afstand fra Mælkevejen målt langs ballonoverfladen. Først beregnes den vinkel, u, som lyset bevæger sig langs ballonens rand, se figuren. Med udvidelseshastigheden fra b får man, at vinklen er givet ved:

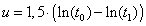
hvor t₁ og t₀ er tidspunkterne ved hhv. lysudsendelsen og lysmodtagelsen. Se beregning af formlen for u.

4. Brug formlen for den „tilbagelagte" vinkel til at finde galaksens afstand ved lysmodtagelsen (nu!), d₀. Find desuden galaksens afstand ved lysudsendelsen, d₁.

Vi har nu beregnet tre forskellige afstande mellem galaksen og Mælkevejen: d₁ og d₀ fra spørgsmål d og afstanden fra spørgsmål c.

5. Brug figuren til at forklare, hvorfor der er så stor forskel på de tre værdier. Diskutér, hvilket af de tre tal, der bedst kan bruges som et mål for afstanden til galaksen.

 

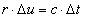
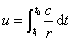
Beregning af formlen for u: Når lyset bevæger sig en lille vinkel Du langs overfladen ved radius r, gælder at den tilbagelagte afstand er givet ved: hvor Dt er det tilhørende tidsrum. Forklar ovenstående formel. Isolér Du i formlen, og gør rede for at den samlede „tilbagelagte" vinkel er givet ved: hvor t1 og t0 er tidspunkterne ved lysudsendelsen og lysmodtagelsen. 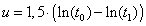Udtryk r som funktion af tiden t, og vis at integralet = den „tilbagelagte" vinkel er givet ved: Vi så i opgave 20, at man får meget forskellige afstande, afhængigt af hvad man forstår ved „afstand". Selv om vores kosmologiske model ser ret primitiv ud, illustrerer den på udmærket måde de helt grundlæggende problemer med at bestemme afstande til meget fjerne galakser. Vi kan dog formentlig få bedre resultater, hvis vi opgiver antagelsen om en jævn udvidelseshastighed. De fleste kosmologer mener nemlig, at rummets udvidelse bremses op. Derfor vil vi også prøve at anvende Einstein-de Sitter modellen for universets udvidelse, der af mange anses for at være det bedste „gæt" på universets virkelige opførsel.