Opgave 1
Regning med rest
Den positive rest, man får, når et helt tal a divideres med et naturligt tal n, betegnes
Hvis r = rest(a,n) kan a skrives a = k · n + r hvor 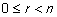 og k er et helt tal. Der gælder at og k er et helt tal. Der gælder at
| rest(a + b,n ) = rest(rest(a,n ) + rest(b,n ),n ) |
(2) |
| rest(a · b,n ) = rest(rest(a,n ) · rest(b,n ),n ) |
(3) |
1. Giv eksempel på, at der ikke gælder
rest(a + b,n ) =rest(a,n )+rest(b,n )
2. Udregn i hånden ved brug af (2) og (3):
rest(66 · 84, 20) og rest(310 , 20)
rest(a,n ) = rest(b,n ) 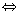 n går op i a - b n går op i a - b |
(4) |

|
Lad p være et primtal, der ikke går op i a. Da gælder
De følgende to opgaver giver beviset for sætningen.
Vi ser på tallene a , 2a , … , (p -1)a og deres rest b1 , b2 , … , bp-1 ved division med p.
| 1. |
Giv et indirekte bevis for at b'erne alle er forskellige og at ingen af dem er 0. Der gælder altså at b'erne er tallene 1 , 2 ,…, p -1 blot i en anden rækkefølge |
| 2. |
Gør rede for at
rest(a · 2a ·…· (p-1)a, p ) =rest(1 · 2 · …· (p-1), p )
og at dette medfører Fermats lille sætning.
|
Sæt p =17. For x tilhørende mængden af hele tal fra 1 til 16 ser vi på funktionerne:
f (x ) = rest(x3,17) og g(x ) = rest(x11,17)
| 3. |
Vis at g ( f ( x )) = x |
Man kan altså kryptere med f og dekryptere med g.
|
Der findes ikke nogen formel til at finde for eksempel primtal nummer 1000 uden at bestemme de foregående, men der er heller ikke nogen enkel metode til bare at afsløre om et tal er et primtal. Vi vil her se på den mest nærliggende metode, nemlig at forsøge at finde divisorer fra neden af.
Opgaverne er formuleret under forudsætning af, at der er en TI-83 lommeregner til rådighed; men opgaven kan nemt tilpasses en CAS lommeregner eller et computerprogram.
Lommeregneren har indbygget funktionen int(x ), der beregner den hele del af x, altså det største hele tal mindre eller lig x. Ved hjælp af denne funktion kan rest(n,k ) beregnes som
Dette udtryk indgår i følgende program PrgmPRIM, der finder ud af om et givet tal N er et primtal, ved at undersøge om nogen af tallene fra 2 til kvadratroden af N går op i N.
: Input "N = ",N
: For (K,2,Int(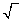 (N))) (N)))
: If N-K*int(N/K)=0
: Then : Disp "NEJ"
: Goto A
: End : End
: Disp "JA"
: Lbl A
|
| 1. |
Undersøg hvor lang tid det tager lommeregneren at køre programmet for hver af følgende værdier af N:
| 1009 |
10007 |
100003 |
1000003 |
10000019 |
og opstil ud fra disse tal en sammenhæng mellem antal cifre og tid. Sammenlign den tid, det ville tage at undersøge et tal med 200 cifre, med universets alder, som anslås at være 14 · 109 år.
|
| 2. |
Udled teoretisk en sammenhæng mellem antal cifre og tid. |
Metoden i programmet er i raffineret form Eratosthenes si (240 f.kr.). I talrækken:
2 , 3 , 4 , 5 , 6 , 7 , 8 , 9, .... , n
udtages det mindste tal 2 og alle egentlige multipla af 2 bortsies:
3 , 5 , 7 , 9 , 11, … , n
dernæst udtages 3 i listen og alle egentlige multipla af det 3 bortsies:
Således fortsættes succesivt med at udtage det mindste tal i listen og bortsi egentlige multipla heraf. Når processen standser, har vi udtaget alle primtal mindre end eller lig n. Metoden kan afprøves i praksis for n = 400 på
|
Opgave 4
For at kunne forstå ideen i AKS-algoritmen får man brug for at
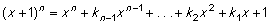 |
(6) |
hvor koefficienterne k i er hele tal, der ifølge binomialformlen kan udregnes som
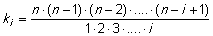 |
(7) |
| 1. |
Udregn (x+1)4 og (x+1)5 ved (6) og (7). |
Der gælder følgende primtals kriterium:
|
Tallet n er et primtal, hvis og kun hvis n går op i samtlige koefficienter i polynomiet
|
|
(8) |
| 2. |
Gør rede for at ovenstående påstand er rigtig. |
Dette elegante primtals kriterium er imidlertid slet ikke til beregningsmæssig nytte. For store n er det umuligt at beregne (x+1)n. Ideen er nu istedet at beregne resten r (x) af 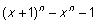 ved polynomiers division med polynomiet x r - 1 for et passende r. Denne rest kan beregnes ved brug af regnereglerne (2) og (3) uden at behøve beregne (x+1)n . Samtidigt gælder (8) i en vis forstand næsten, når ved polynomiers division med polynomiet x r - 1 for et passende r. Denne rest kan beregnes ved brug af regnereglerne (2) og (3) uden at behøve beregne (x+1)n . Samtidigt gælder (8) i en vis forstand næsten, når 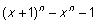 erstattes med r (x), som det antydes af eksemplet i de følgende opgaver: erstattes med r (x), som det antydes af eksemplet i de følgende opgaver:
| 3. |
Når r =2 er det muligt at bestemme r (x ) uden at lave divisionen. Sæt 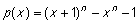 . Gør rede for, at r (x) er et førstegradspolynomium, hvis graf går gennem (-1, p(-1)) og (1, p(1)) og at . Gør rede for, at r (x) er et førstegradspolynomium, hvis graf går gennem (-1, p(-1)) og (1, p(1)) og at 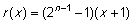 når n er ulige. når n er ulige. |
| 4. |
Gør rede for at n går op i koefficienterne i r (x), hvis n er et primtal. |
Der findes desværre n, der ikke er primtal, for hvilke n går op i samtlige koefficienter i polynomiet 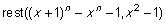 . Det mindste er 341. Men metoden kan reddes ved så at se på rest ved division med . Det mindste er 341. Men metoden kan reddes ved så at se på rest ved division med 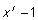 for større primtal r end 2. Vi stopper imidlertid her, hvor hovedideen i AKS-algoritmen er illustreret. for større primtal r end 2. Vi stopper imidlertid her, hvor hovedideen i AKS-algoritmen er illustreret.
| 5. |
Udregn rest(2340,341) ved at bruge 210 som mellemstation. |
Det afgørende ved AKS-algoritmen er, at tidsforbruget ikke vokser eksponentielt som funktion af antallet af cifre, men som en potensfunktion (eller polynomium).

|
Opgave 5
Euklids algoritme
Primtallene er byggeklodserne i systemet af hele tal. Ethvert helt tal kan nemlig faktoriseres i et produkt af primtal - endda på en entydig måde. Ved hjælp af primtalsfaktorisering kan man for eksempel i princippet bestemme den største fælles divisor for to tal a og b, som betegnes sfd(a,b ).
| 1. |
Faktoriser 294 og 60, og angiv den største fælles divisor |
I praksis er det ikke muligt at finde største fælles divisor for meget store tal på denne måde, da der er ikke nogen kendt effektiv måde at faktorisere på. Vi vil nu se på Euklids algoritme, der i et overkommeligt antal trin finder den største fælles divisor for to tal. Algoritmen bygger på følgende:
| sfd(a,b ) = sfd(b,rest(a,b )) |
(9) |
Eksempel:
Når a = 294 og b = 60 giver Euklids algoritme:
294 = 4 · 60 + 54
60 = 1 · 54 + 6
54 = 9 · 6 + 0
|
Største fælles divisor for 6 og 54 er altså 6 (da 6 går op i 54), og 6 er derfor også største fælles divisor for 294 og 60.
Vi ser nu på to tal a og b, for hvilke den største fælles divisor er 1. Vi skal se, hvordan man kan bestemme hele tal x og y, således at
eller med andre ord: så a ·x har resten 1 ved division med b. Metoden, der går ud på først at opskrive Euklids algoritme, og dernæst i en vis forstand regne baglæns, illustreres med følgende eksempel:
Når a = 7 og b = 23 giver Euklids algoritme:
23 = 3 · 7 + 2
7 = 3 · 2 + 1
I hver af ligningerne isoleres det sidste led:
2 = 23 - 3 · 7
1 = 7 - 3 · 2
I den nederste ligning erstattes 2 med højresiden i den ovenstående:
1 = 7 - 3 · (23 - 3 · 7) = - 3 · 23 + 10 · 7
Der gælder altså at 1 = x · 7 + y · 23 for x =10 og y = -3.
|
| 2. |
Bestem et tal x, således at 11 · x har resten 1 ved division med 62. |
| 3. |
Bestem hele tal x og y, således at 1000 = 7x + 11y |
Reference:
Johan P. Hansen og Henrik Spalk: Algebra og talteori , Gyldendal(2002)
|
Opgave 6
Nøglekonstruktion i RSA-system
Første trin i opbygningen af et RSA-system er at vælge tallet n, der skal være et produkt af to primtal p og q. Tallet (p - 1) • (q - 1) kaldes f.
Andet trin består i at vælge tallet k, der skal være en del af den offentlige nøgle. Det eneste krav til k er, at der ikke må være noget helt tal større end 1, der går op i både k og f.
Tredje trin består i at vælge det hemmelige nøgletal d. Tallet d skal vælges således at
rest(k · d, f ) = 1 (10)
| 1. |
Sæt (k,n ) = (3,33). Bestem en hemmelig nøgle d. |
| 2. |
Sæt (k,n ) = (5,51). Bestem en hemmelig nøgle d. |
| 3. |
En elev har fødselsdag i april. Eleven vil ikke direkte oplyse hvilken dag, men fortæller, at hvis man krypterer med (k,n ) = (5,51) får man 8. Bestem fødselsdagen.. |
Reference:
P. Landrock og K. Nissen: Kryptologi, Abacus (1997)
|
Opgave 7
Elliptiske kurver
| 1. |
Betragt den elliptiske kurve med ligningen
Beregn koordinaterne til P + Q og til 2P, når P =(1,1) og Q =(3,5).
|
| 2. |
Kurver med en ligning af formen
kan for specielle værdier af a og b have punkter, hvor der ikke er en tangent. Det sker, hvis højresiden af ligningen har en dobbeltrod, det vil sige, hvis der findes tal a og b så
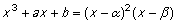 |
(11) |
Vis, at (11) medfører, at
Tegn kurven med ligningen
og undersøg specielt kurven omkring punktet (1,0).
|
|
|
Opgave 8
Elliptiske kurver modulo p
At to tal a og b har samme rest ved division med p skrives
| 1. |
Bestem samtlige løsninger (x,y ) modulo 5 til ligningen
|
Når en meddelelse skal repræsenteres som et punkt på kurven, omsættes meddelelsen til at tal, og der vælges et punkt, hvis x -koordinat er lig med eller tæt på dette tal. For at finde y -koordinaten indsættes i højresiden af kurveligningen og regnes modulo p, hvilket giver en ligning af typen
Resultatet i den følgende opgave kan bruges til at afgøre om (12) har en løsning:
| 2. |
Benyt Fermats lille sætning til at vise at
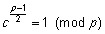 |
(13) |
|
Hvis (12) har løsninger kan en løsning bestemmes ved brug af resultatet i den følgende opgave, når p har rest 3 ved division med 4.
| 3. |
Benyt Fermats lille sætning til at vise at
er løsning til (12) hvis (13) er opfyldt. Bemærk at eksponenten i (14) kun er et helt tal når p har rest 3 ved division med 4.
|
| 4. |
har en løsning og bestem en løsning.
|
Ud fra den geometriske beskrivelse af addition af punkter kan man udlede følgende koordinatudtryk. Lad P (x 1 , y 1) og Q (x 2 , y 2) og P + Q = (x 3 , y 3) så er
| (x 3 , y 3) = (s 2 -x 1 - x 2 , - y 1 + s(x 1 - x 3)) |
(15) |
Her er s hældningskoefficienten til linjen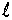 , og formlen for s afhænger af om , og formlen for s afhænger af om 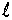 er sekantline (P ≠ Q ) eller tangentlinie (P =Q ): er sekantline (P ≠ Q ) eller tangentlinie (P =Q ):
sekantlinie: 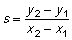 |
tangentlinie: 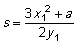 |
Når der regnes modulo et tal p, skal p være et primtal for at division kommer til at fungere fornuftigt.
| 5. |
Bestem  , som er løsningen til ligningen 5 ·x = 1 modulo 17. Udregn dernæst , som er løsningen til ligningen 5 ·x = 1 modulo 17. Udregn dernæst  . .
|
|
|