Inden for de sidste 10 år er man begyndt at kryptere ved hjælp af elliptiske kurver - kurver, der har ligninger på formen
|
|
(1)
|
hvor a og b er tal, således at kurverne har tangenter i alle punkter.
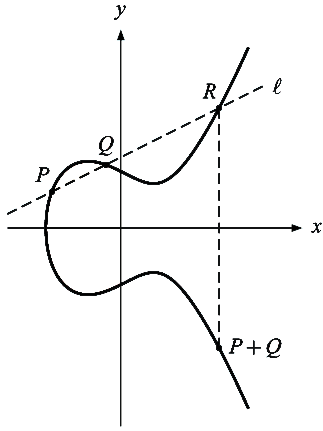
En af de specielle egenskaber ved disse kurver er, at man på en geometrisk måde kan addere punkter på kurven. Lad P og Q være to punkter på kurven. Hvis P ≠ Q betegner ![]() sekantlinien gennem punkterne, og hvis P = Q er
sekantlinien gennem punkterne, og hvis P = Q er ![]() tangentlinien til kurven i P. Antager vi, at
tangentlinien til kurven i P. Antager vi, at ![]() ikke er lodret, så skærer
ikke er lodret, så skærer ![]() den elliptiske kurve i præcis et ekstra punkt R. Dette punkt spejles i x-aksen, og vi opnår resultatet af additionen, nemlig punktet P + Q, se figuren.
den elliptiske kurve i præcis et ekstra punkt R. Dette punkt spejles i x-aksen, og vi opnår resultatet af additionen, nemlig punktet P + Q, se figuren.
Det er let at udlede formler for, hvordan koordinaterne til P+Q kan beregnes ud fra koordinaterne til P og Q; disse beregningsformler er simple på den måde, at der kun indgår de sædvanlige fire regningsarter. Skæringspunktet mellem ![]() og kurven kan nemlig beregnes ved at løse en trediegradsligning, hvor man på forhånd kender to rødder.
og kurven kan nemlig beregnes ved at løse en trediegradsligning, hvor man på forhånd kender to rødder.
I grove træk foregår krypteringen på følgende måde. Der vælges et fast punkt Q på kurven. Meddelelsen omsættes til tal, som så igen omsættes til et punkt på kurven. Den krypterede tekst fremkommer ved addere Q til dette punkt.
I praksis er der imidlertid et par knolde på vejen. En computer regner kun med et endeligt antal decimaler, så de punkter på kurven man kan bruge, skal kunne angives eksakt med endeligt mange decimaler, og den slags punkter kan det godt være svært at finde nok af, selv i tilfælde hvor der er uendelig mange.
Elliptiske kurver modulo et primtal p
Løsningen på dette problem er at vælge et i praksis stort primtal p og regne modulo p. Det vil sige, at et par af hele tal (x,y) er løsning til ligningen (1), hvis bare venstresiden og højresiden giver samme heltalsrest ved division med p.
For eksempel er (3,2) løsning til ligningen ![]() modulo 7, da højresiden giver 25, som har rest 4 ved division med 7.
modulo 7, da højresiden giver 25, som har rest 4 ved division med 7.
På denne måde bliver der mange løsninger. Antallet af løsninger, hvor både x og y er et af de hele tal fra 0 til p -1, er af samme størrelsesorden som p. Det betyder, at hvis man prøver sig frem ved at indsætte x lig med 0,1,2,… vil i gennemsnit cirka hver andet forsøg give to løsninger.
To løsninger P og Q modulo p kan adderes ved at bruge de tidligere nævnte beregningsformler for P+Q, idet der nu regnes modulo p.
Kryptering ved hjælp af elliptisk kurver, som betegnes ECC, kan foregå som beskrevet i eksemplet nedenfor.
Her betegner dG et punkt af formen G+G+… + G, hvor d er antallet af led i summen.
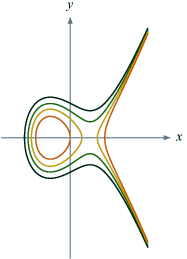 |
Elliptiske kurver med ligningen
hvor b = 0, 0,3 , 0,6 , 1 |
Det diskrete logaritmeproblem
Kan den hemmelige nøgle d bestemmes udfra punkterne G og dG, kan systemet brydes. At finde d er at løse det diskrete logaritmeproblem - sikkerheden beror altså på, at det diskrete logaritmeproblem er uløseligt i praksis!
EksempelLad p = 13 og betragt den elliptiske kurveligning Tabellen viser at ligningen d (12,1) = (6,9) modulo p har løsningen d = 6.
I virkelige anvendelser vil d være så stor, at den her anvendte metode er helt og aldeles uegnet. Faktisk er der ikke nogen kendt effektiv metode - det er hele sikkerheden i kryptosystemet! |
NøglekonstruktionPersonen A laver et nøglepar ved at vælge en elliptisk kurve E med et punkt G samt et tal d.
|
KrypteringPersonen B vil sende en besked til A.
|
DekrypteringModtageren A dekrypterer :
|
Fordele ved ECC
ECC kræver mindre lagerplads og energi, fordi man med kortere nøgler kan opnå den samme sikkerhed. En nøglelængde på 2048 i RSA modsvares for eksempel af en på kun 224 i ECC. Derfor kan man lave stærke kryptografiske løsninger på mindre platforme, for eksempel mobiltelefoner og smartcards.
ECC er standardiseret. For eksempel angiver The National Institute of Standards and Technology (NIST) standarder for kryptografiske metoder som de offentlige myndigheder i USA kan anvende. Blandt andet anvises 15 elliptiske kurver, der må bruges. Også i Europa og Japan er der standarder.