Opgave 07: Rødforskydning og hastighed

Vi vil nu forsøge at finde en sammenhæng mellem en galakses rødforskydning, z og den hastighed, v hvormed den tilsyneladende bevæger sig bort fra os på grund af rummets udvidelse.

Vi går ud fra, at vi (Mælkevejen) ligger stille, og at galaksen, der til tidspunktet t = 0 befinder sig i afstanden d₁, udsender lys med bølgelængden l₁. Efter tidsrummet, t er galaksen nået ud til afstanden d₂, og lyset ankommer derfor til Mælkevejen rødforskudt med bølgelængden l₂.

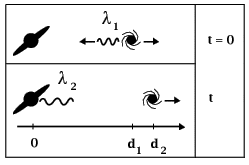
Da galaksen i det betragtede tidsrum, t har bevæget sig strækningen d₂ - d₁ , gælder:

d₂ - d₁ = v · t.

Lyset har bevæget sig strækningen d₁ givet ved:

d₁ = c · t.  Advarsel

Ud fra udtrykket for den kosmologiske rødforskydning fra opgave 6 kan vi nu udtrykke z ved v og c:

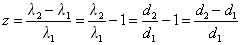
Altså

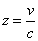
1. En galakse har en rødforskydning på 0,08. Med hvilken hastighed fjerner den sig fra os? Hvad er afstanden til den? Hvor langt har den fjernet sig fra os, mens lyset var undervejs? Hvor stor en procentdel udgør det af dens afstand?

2. Hvor langt har galakserne i tabellen i opgave 2 fjernet sig fra os, mens lyset har været undervejs?

Advarsel Den strækning, som lyset har bevæget sig i tidsrummet t, er i virkeligheden større end d1, fordi rummet udvider sig, mens lyset er undervejs. Formlen z = v/c kan derfor kun bruges for de galakser, der er så tæt på os (dvs. har så små rødforskydninger), at den fejl, man herved begår, kan negligeres. I praksis går grænsen omtrent ved z = 0,1. For galakser med rødforskydninger større end z = 0,1 bliver afstandsbegrebet problematisk. Her bliver man nødt til at skelne mellem 1) afstanden til en galakse på det tidspunkt, hvor det lys, vi observerer fra den, blev udsendt og 2) afstanden til galaksen på det tidspunkt, hvor vi modtager lyset fra den. Som det vil fremgå af opgaverne i afsnittet Kosmologiske afstande, er der for galakser med store rødforskydninger meget stor forskel på de to afstandsmål.