
Opgave 18: Sandwichmodellen
Denne opgave bygger på sandwichmodellen.
For de yngste ca. 50.000 år har det været muligt at tælle årslagene i GISP2-boringen (se opgave 3). Vi kan derfor undersøge sandwichmodellen ved at se på dateringen af den øverste del af isen.
Den omtalte datering af GISP2-boringen fremgår af følgende diagram:
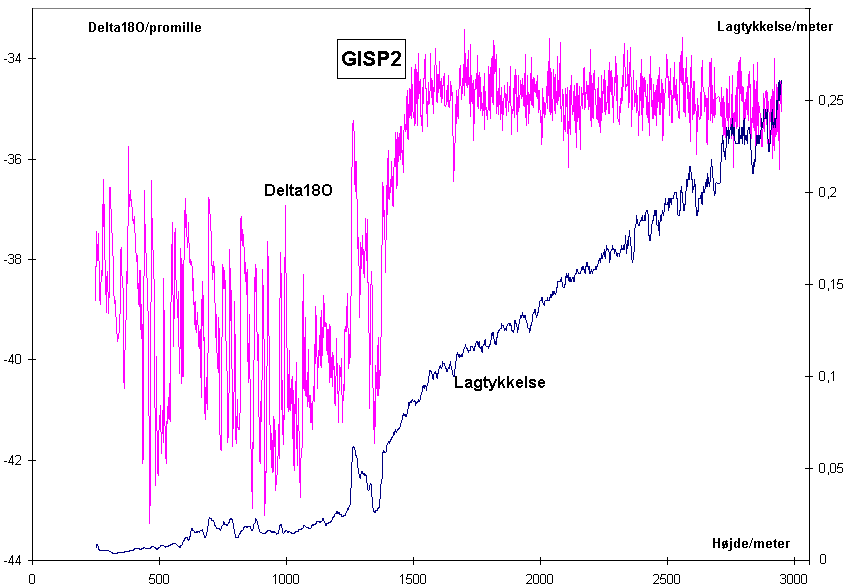
(Download datafilen giso18.xls / giso18.zip og diagramfilen diagram.xls / diagram.zip).
En stor del af de følgende opgaver kan med fordel løses ved at arbejde direkte i regnearket, vælg selv!
Først skal vi se på vores nuværende mellemistid, dvs. de sidste ca. 11.000 år
-
Vælg mindst 12 sammenhørende værdier for isens alder og dybde jævnt fordelt i intervallet [100 m;1500 m]. Omregn dybden til højde, y, over grundfjeldet (samlet højde er H = 3050 meter)
-
Undersøg om y afhænger eksponentielt af alderen ved hjælp af logaritmepapir.
-
Tegn bedste rette linie og udregn parameteren a/H.
-
For de valgte data i a. findes lagtykkelsen ud fra filens oplysninger. Lagtykkelsen beregnes i antal meter pr. år.
-
Undersøg om der er en lineær sammenhæng mellem lagtykkelsen og højden y. Find i så fald liniens hældning a/H og sammenlign med resultatet fra c.
Vi vil nu se på den ældste del af GISP2-isen, der er dateret. Det drejer sig om den seneste istid med nogle perioder ind imellem med varmere klima omkring. Isen fra denne periode ligger ca. i intervallet [1600m; 2800m].
-
Undersøg om der i denne periode er en eksponentiel sammenhæng mellem højde og alder.
-
Undersøg om der i denne periode er en lineær sammenhæng mellem lagtykkelsen og højden y.
I f. og især g. har du sikkert set, at modellen ikke passer ret godt.
I diagrammet ses lagtykkelsen og d18O som funktion af højden over grundfjeldet. Istiden slutter ca. i højden 1400 meter.
-
Brug diagramemt til at forklare, hvorfor den simple sandwichmodel ikke kan bruges i istiden. Overvej, hvordan modellen skal modificeres for at give et bedre resultat.