Sandwichmodellen

Som nævnt under temaerne anvender man til at datere isen i store dybder en kombination af målinger af støvindholdet og modeller for isens flydebevægelse. Den simpleste af den slags modeller kaldes sandwichmodellen. Selv om den bygger på en række meget enkle forudsætninger, kan den alligevel forklare en masse fundamentale iagttagelser vedrørende bevægelsen af store iskapper.

  • Download datafilen gisp2O18.xls / gisp2O18.zip.
  • Download datafilen gisp2SO4.xls / gisp2SO4.zip.

    • En kæmpe-islagkage

    Den grønlandske indlandsis kan beskrives som en enorm islagkage. Med nogle få forudsætninger kan vi opstille en simpel model for isens bevægelse. Det giver os nogle enkle formler, der nøjagtigt beskriver isens alder og bevægelse.

    Nedenfor ses en figur som i temaet Kæmpemæssig islagkage... Her er indlagt en x-akse henad langs klippegrunden og en y-akse opad langs isdeleren.

    I "Sandwich-modellen" fås en eksponentiel sammenhæng mellem y = isens højde over klippen og t = isens alder:

    y(t)

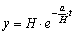
    H er isens samlede højde og a er den årlige istykkelse, der falder (som sne).

    Desuden er der proportionalitet mellem A = tykkelsen af hvert års-lag og isens højde over klippen:

    A(y)

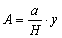
    I de følgende opgaver vil vi sammenligne sandwich-modellen med målinger fra indlandsisen.

    Men først vil vi præsentere modellen og udlede formlerne:

    Forudsætningerne for modellen er:

    1. Isen er usammentrykkelig
    2. Den årlige tykkelse af isen, der lægger sig på iskappen, er konstant (konstant nedbør)
    3. Isens vandrette bevægelse afhænger ikke af dybden
    4. Den mængde nedbør, der falder på isen, forsvinder igen som isbjerge og afsmeltning ved randen. Iskappens form er derfor konstant.

    På figuren nedenunder ses et udsnit af indlandsisen. Vi regner med at udsnittet har en tykkelse på 1 km (ind i papiret).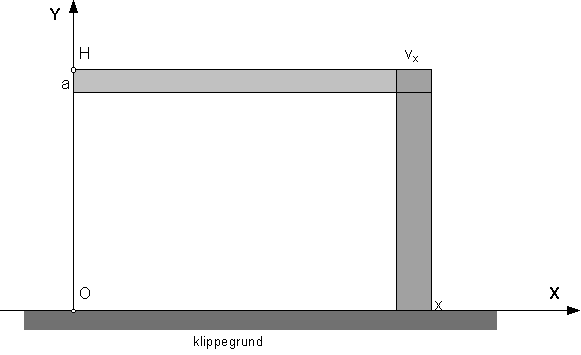Udsnit af indlandsisen

    Vi ser først på et udsnit i hele iskappens højde::

    Den årlige is-nedbør svarer i afstanden x fra isdeleren til et volumen på:

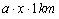
    Volumen af isnedbør i afstanden x

    Samtidig flyder isen ud mod kysten med et årligt volumen på:

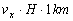
    Isvolumen

    der forlader det viste udsnit. vx er isens vandrette hastighed i meter pr. år.

    Da iskappens form er konstant, skal de to rumfang være lige store:

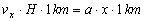
    Ens rumfang

    Eller:

    (1)

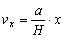
    (1)

    Vi ser nu på et udsnit i højden y (jf. figuren):

    Isens lodrette hastighed vy giver, at der pr. år tilføres et volumen is på:

    - vy x

    Bemærk at vy er negativ.

    Samtidig flyder der årligt ud af udsnittet:

    vx y

    Da vi regner isen for at være usammentrykkelig, fås:

    - vy x = vx y      (2)

    Ved at kombinere (1) og (2) fås:

    (3)

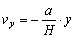
    eller

    (3)

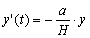
    (3)

    Man kan vise, at løsningen til (3) er en eksponentialfunktion:

    (4)

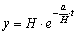
    (4)

    hvor konstanten H er bestemt af at y = H til t = 0.

    Formlen (4) viser os, at isens højde over klippen aftager eksponentielt med alderen. Bemærk at højden ikke afhænger af x, dvs. at is med samme alder ligger i et vandret lag, deraf navnet "Sandwich-modellen".

    Vi ser desuden, hvordan et islag med tykkelsen H aftager med tiden. Det samme må gælde om ethvert lag af is, jf. (3), så årlaget med tykkelsen a har til tiden t tykkelsen:

    (5)

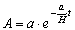
    (5)

    der sammen med (4) giver:

    (6)

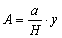
    (6)

    Opgave

    Nedbøren på Grønland afhænger meget af geografien. Antag af den årlige nedbør giver en istykkelse øverst på iskappen på a = 0,25 m/år, og at isens tykkelse er: H = 3000 m.

    Find tykkelsen af et årslag og alderen af isen i dybderne:

    100 m, 500 m, 1000 m, 2000 m, 2500 m, 2800 m, 2950 m