Øvelser i fysisk modeldannelse

Hold musen over øvelsesnummeret for at se titlen

Model 6

Modeller for afslidninq af meteoritten under faldet

Nu ved vi, at det er meget store effekter, der omsættes i 20-30 kilometers højde under et meteorfald. En detaljeret redegørelse for, hvilke former for energi denne omsætning bruger, er uhyre kompliceret og næppe forstået i detaljer af eksperterne. Vi kan alligevel med en række simple antagelser udvide modellen til at tage hensyn til, at meteoritten mister masse under faldet.

Vi skal blot antage at en brøkdel, b, af bremsekraftens effekt går til fordampning af meteoritmaterialet.

Denne brøkdel ved vi intet om i forvejen. Men vi ved, at meteoritter i kg-størrelsen faktisk kan overleve faldet og faktisk bliver slidt noget under faldet. Så må vi tilpasse b så dette sker. Dette kaldes at kalibrere modellen på virkeligheden.

Vi får så et bud på brøkdelen b, og kan spørge om dette er rimeligt. Måske kan teoretikere komme op med en formel, der siger, hvor stor b burde være. En sammenligning vil vise, om de skyder helt ved siden af.

Når vi skal regne på denne model, må vi indføre nogle nye parametre og nye variabelkolonner. Vi må indføre brøkdelen, b (som vi intet ved om i forvejen) og fordampningsvarmen, L, som vi kan få et godt bud på fra Databogen. Massen skal nu være variabel. Om overfladearealet også skal være det, er en smagssag, alt efter hvordan man forestiller sig, at meteoritten ser ud under faldet. Forestiller man sig meteoritten som en kugle, kan man bruge kugleformler til at udregne radius og areal som funktioner af massen. Det giver kvalitativt de samme resultater at forestille sig meteoren som en terning, der slides af på den ene flade.

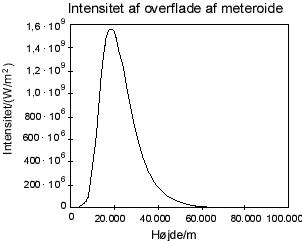
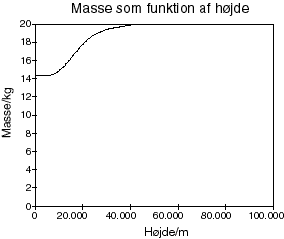
Indret f.eks. regnearket med kolonner for den intensitet, der afsættes på overfladen og med massen af meteoritten.

Forsøg at udlede, at formlen for massetabet i løbet af tidsskridtet Dt er

Dm = I_eff · A · Dt / L

Med en fordampningsvarme på 6,5 MJ/kg og en brøkdel, b på 0,01 ser det således ud:

 

 

1. Prøv at sammenligne den maksimale intensitet på overfladen af meteoritten med intensiteten i en bunsenbrænderflamme. Til dette overslag kan man regne med, at bunsenbrænderen leverer en effekt på 1000 W gennem et areal på 1 cm².