Model 3

Computermodel: Bremsning af en meteorit

Når en meteorit bremses ned gennem atmosfæren, ændrer hastigheden sig jo klart nok. Dermed ændrer bremsekraften sig. Men bremsekraften ændrer sig også undervejs, fordi atmosfærens densitet ændrer sig; lufttrykket falder jo med højden. I det følgende vil vi vise, hvordan man kan lave en computermodel i et simpelt regneark, der kan demonstrere, hvor bremsekraften er størst, og hvor store accelerationer meteoritten kommer ud for.

Senere vil vi udbygge den med simple antagelser for hvor meget masse, der mistes undervejs.

I første omgang skal vi bruge følgende parametre:

• højden over jorden = x,
• starthøjden = x₀= 200 km
• luftens densitet ved Jorden = d₀= 1,3 kg/m³
• halveringshøjde for luftens densitet = H = 5000 m
• meteorittens masse = m₀= 20 kg
• meteorittens tværsnitsareal = A = (0,018 m² for en kubisk jernmeteorit)
• meteorittens begyndelsesfart = v₀ = 20 km/s
• meteorittens fart = v, som afhænger af
• tiden = t, der skrider frem med
• tidsskridt =Dt.

Konstanterne skriver man ind i enkeltceller i regnearket. Det er en god ide at navngive cellerne med de navne, der er foreslået ovenfor.

Nu opretter man kolonner for alle de størrelser, der ændrer sig i løbet af faldet. Det er tiden, højden, luftens densitet, hastigheden og accelerationen. Første række i disse kolonner er speciel derved, at startværdierne sættes ind i form af referencer til de enkeltceller, hvor tallene er sat ind, mens f.eks. densiteten beregnes som en formel.

Nyeste række er beregnet ud fra den forudgående. For at komme fra en række til den næste bruges overgangsformlerne i sidste kolonne.

Størrelse	Beskrivelse	Formel
Tiden	D t lægges til den gamle tid.
Højden	Vi regner med konstant hastighed i det enkelte tidsskridt, så meteoritten har bevæget sig strækningen Dx lig farten gange Dt.
Densiteten	Beregnes som en eksponentiel udvikling af højden.
Accelerationen	er tyngdeaccelerationen minus bremseaccelerationen. Denne sidste er bremsekraften divideret med meteorittens masse.
Farten	er den tidligere fart plus fartændringen givet ved accelerationen gange tidsskridtets længde.

I regnearket tastes formlerne ind således:

Hent modellen i FPro - eller i Excel 97 -eller i Excel 5 - eller i Excel 3.

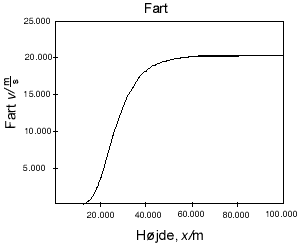
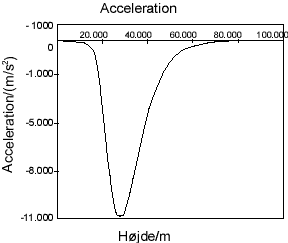
Og den sidste formellinie kopieres de næste ca. 500 rækker ned. Nu er beregningen komplet, og man kan få grafer f.eks. af fart og acceleration som funktioner af højden.

Med følgende startparametre får man graferne vist nedenfor.

	A	B
7	Konstanter i SI enheder
8
9	Startmasse af meteorit, m0	20
10	Densitet af meteorit	8000
11	Begyndelseshastighed, v0	20000
12	I højde, x0	200000
13	Lufttæthed ved jord, d0	1,3
14	Halveringshøjde, H	5000
15	Luftmodstandskoefficient, cv	1
16	Tidsskridt, Dt	0,05
17	Tværsnitsareal, A	0,018420157