En meterstok spændes fast i den ene ende, og belastes med lodder eller kraftmåler i den anden.
Der gælder da, at nedbøjningen x som funktion af afstanden z fra fastgøringspunktet er givet ved :
hvor F er kraften, L er den samlede længde, w er bredden, h er højden og E er Youngs modul, der er en materialekonstant.
Linealen har følgende højde: h = 0,025 m og bredde: w = 0,005 m.
I et forsøg har man valgt L = 0,50 m og belastningen var m = 0,70 kg . Man målte følgende værdier:
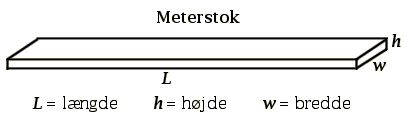
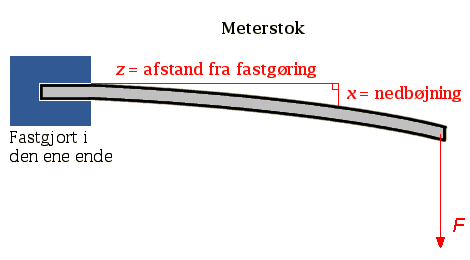
z/ m
0,15
0,20
0,35
0,30
0,35
0,40
0,45
0,50
x/ m
0,007
0,013
0,020
0,028
0,037
0,046
0,055
0,065
Brug grafregneren til at undersøge om x er et tredjegradspolynomium i z:
x = a·z3 + b·z2 + c·z + d
hvor c = d = 0, og b/a = -3·L. Brug a til at beregne E.
I en ny undersøgelse interesserer man sig udelukkende for nedbøjningen i den frie ende.
Vis, at nedbøjningen i den frie ende - dvs. for z = L - er givet ved.
I forsøget er linealen belastet med en masse på m = 0,500 kg. Nedbøjningen er målt som funktion af L
L/ m
0,50
0,60
0,70
0,80
0,90
x/ m
0,046
0,080
0,127
0,189
0,270
Undersøg, om x er proportional med L3. Bestem E ud fra målingerne. Ser det rimeligt ud?
Beregn nedbøjningen for en lineal med samme E og L = 0,70 m , m = 0,50 kg, h = 0,025 m og w = 0,01 m.
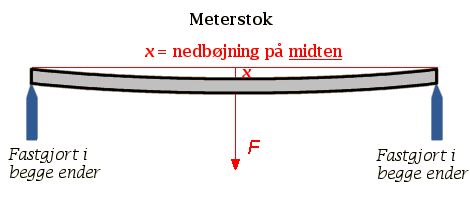
Hvis man i stedet havde lagt linealen med støttepunkter i begge ender og målt nedbøjningen på midten, ville formlen for nedbøjningen se sådan ud :
Vis, hvordan man kommer fra udtrykket i b til det ovenstående udtryk ved at opfatte linealen som to linealer. Beregn nedbøjningen, hvis L = 0,90 og m = 1,0 kg.
